Obsah obdĺžnika (kalkulačka)
Kalkulačka obsahu obdĺžnika umožňuje vypočítať obsah na základe rôznych vstupov – podľa strán, uhlopriečky a strany, obvodu s pomerom strán alebo súradníc vrcholov.
Obsah obdĺžnika ak je známa dĺžka a šírka strany
Obsah obdĺžnika ak je známa dĺžka uhlopriečky a jedna strana
Obsah obdĺžnika ak je známy obvod a pomer strán a:b
Obsah obdĺžnika ak sú známe súradnice 4 vrcholov (Shoelace vzorec)
Vzorce pre výpočet obsahu obdĺžnika
Obsah obdĺžnika ak je známa dĺžka a šírka strany
S = a x b
Kde:
- a = dĺžka strany obdĺžnika,
- b = dĺžka strany obdĺžnika.
Príklad: Ak máme dĺžku strany a 5 cm a dĺžku strany b 3 cm, tak obsah (S) = a x b = 5 x 3 = 15 cm2.
Obsah obdĺžnika ak je známa dĺžka uhlopriečky a jedna strana
V tomto prípade potrebujeme vypočítať dĺžku ďalšej strany podľa vzorca:
Dĺžka zvyšnej strany = √[d^2−Dĺžka známej strany^2]
Kde:
- d = dĺžka uhlopriečky.
Vypočítaním druhej strany môžeme doplniť do klasického vzorca pre výpočet obsahu obdĺžnika S = a x b.
Obsah obdĺžnika ak je známy obvod a pomer strán a : b
Ako vieme, tak obvod obdĺžnika vypočítame ako:
O = 2 * (a + b)
Kde:
- a = dĺžka strany obdĺžnika,
- b = dĺžka strany obdĺžnika.
Povedzme, že pomer strán je 2:3. V takom prípade si dĺžky strán môžeme vyjadriť ako a = 2x a b = 3x, kde x je neznáma hodnota, ktorá predstavuje spoločný násobok základných dĺžok strán. Takto zachováme pomer strán, aj keď nepoznáme ich konkrétnu veľkosť.
Obvod vieme vyjadriť ako O = 2 * (2x + 3x) = 10x -> x = O / 10
Teraz, ak máme vyjadrený pomer strán pomocou obvodu, tak vieme vypočítať obsah:
Príklad: Máme obvod napr. 50 cm, pomer strán 2 : 3
Riešenie:
- Pomocou vzorca pre obvod a pomerom strany vypočítame, čomu sa rovná x
- x = O / 10 (vyjadrený vyššie cez pomer strán)
- x = 50 / 10 = 5 =>
- strana a = 2x = 2 x 5 = 10
- strana b = 3x = 3 x 5 = 15
- Vypočítali sme dĺžky obidvoch strán zo vzorca pre obvod a pomeru strán
- Výsledné dĺžky doplníme do klasického vzorca pre výpočet obsahu: S = a * b = 10 x 15 = 150 cm2.
Obsah obdĺžnika ak sú známe súradnice 4 vrcholov (Shoelace vzorec)
S = ½ × |(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) − (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)|
Kde:
- (xi, yj) sú súradnice vrcholov v poradí (v smere alebo proti smeru hodinových ručičiek).
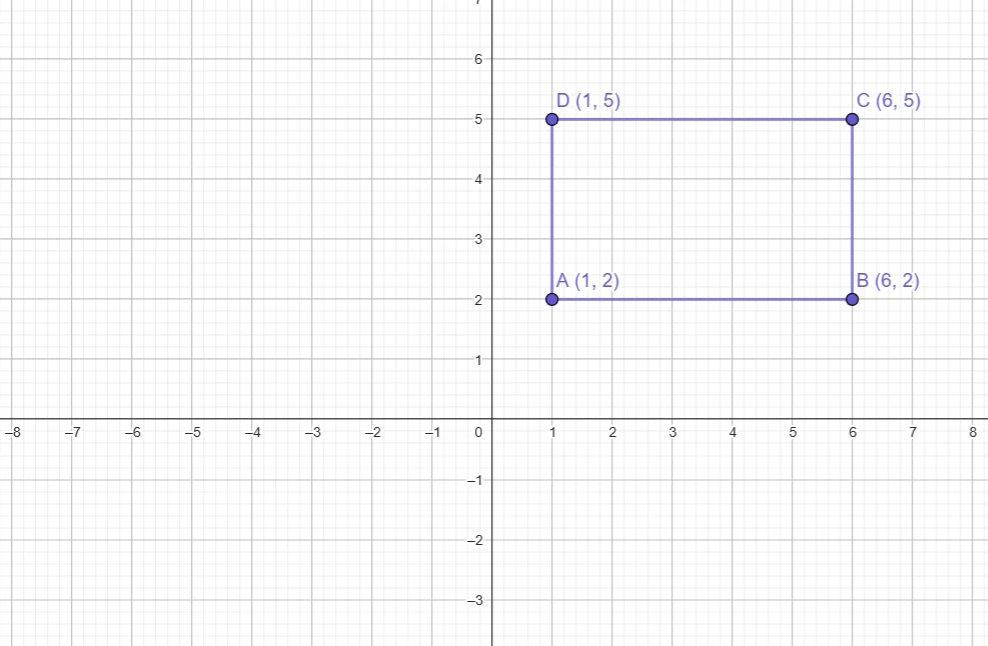
Príklad:
Máme body:
- A (1,2)
- B (6,2)
- C (6,5)
- D (1,5)
Vypočítajme obsah takého obdĺžnika. Dosadíme do vzorca:
S = ½ × |(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) − (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)|
S = ½ × |(1 x 2 + 6 x 5 + 6 x 5 + 1 x 2) − (6 x 2 + 6 x 2 + 1 x 5 + 1 x 5)|
S = ½ × |(2 + 30 + 30 + 2) – (12 + 12 + 5 + 5)
S = ½ x |64 – 34|
S = ½ x 30 = 15
Výsledok: Obsah obdĺžnika je 15 štvorcových jednotiek.
Praktický príklad obsahu obdĺžnika
Chceme položiť dlažbu v obývačke, ktorá má rozmery 6 metrov na dĺžku a 4 metre na šírku. Koľko štvorcových metrov dlažby budeme potrebovať?
Riešenie:
Obsah obdĺžnikovej podlahy vypočítame podľa vzorca:
S = a x b
Kde:
- a = 6 m (dĺžka miestnosti),
- b = 4 m (šírka miestnosti).
Dosadíme do vzorca: S = 6 x 4 = 24 m2
Výsledok: Na celú podlahu obývačky budeme potrebovať 24 m² dlažby.
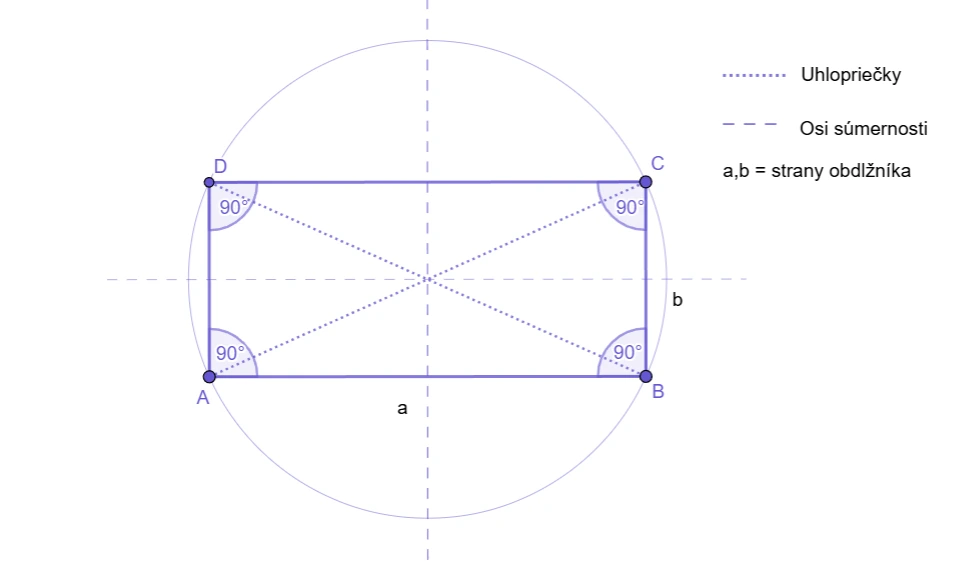
Vlastnosti obdĺžnika
- protiľahlé strany sú rovnobežné a rovnako dlhé,
- susedné strany sú na seba kolmé,
- všetky vnútorné uhly sú pravé,
- uhlopriečky sa rozpoľujú v strede,
- je stredovo súmerný podľa priesečníka uhlopriečok,
- opísaná kružnica prechádza vrcholmi obdĺžnika.
Najčastejšie otázky
Na výpočet obsahu potrebuješ poznať dve navzájom kolmé strany obdĺžnika. Ak poznáš len obvod, uhlopriečku alebo súradnice vrcholov, dá sa obsah dopočítať pomocou doplnkových vzorcov.
Áno, ale iba ak poznáš dve rôzne strany obdĺžnika. V prípade štvorca sa používa zjednodušený vzorec S = a2, keďže všetky strany sú rovnaké.
Shoelace vzorec je matematický algoritmus na výpočet obsahu mnohouholníka pomocou súradníc vrcholov. Používa sa, keď sú známe všetky štyri vrcholy obdĺžnika v kartézskej sústave.
Ak zdvojnásobíš dĺžku jednej strany, obsah sa tiež zdvojnásobí. Ak však zdvojnásobíš obe strany, obsah sa zväčší štyrikrát, keďže rastie exponenciálne: S = 2a x 2b = 4ab
Skontroluj, či protiľahlé strany sú rovnobežné a rovnako dlhé, a či všetky vnútorné uhly sú pravé (90°). V kartézskej rovine to vieš overiť pomocou smerových vektorov a skalárneho súčinu.
Nie. Obdĺžnik má stredovú symetriu, ale nie diagonálnu ako štvorec. To znamená, že uhlopriečky sa síce pretínajú v strede, ale nie sú osami symetrie.
Zdroje:
- Obdĺžnik je rovinný geometrický tvar: https://www.bilingval.sk/_public/files/page/401/clil3.pdf
- Základné prvky a vlastnosti obdĺžnika, konštrukcia obdĺžnika 5. ročník, 13. 04. 2021: https://suborypreziakov.szm.com/zakladne_prvky_a_vlastnosti_obdlznika_konstrukcia_obdlznika.pdf
- Obdĺžnik: https://sk.wikipedia.org/wiki/Obd%C4%BA%C5%BEnik