Kalkulačka objemu

Kalkulačka objemu nám umožní rýchlo a jednoducho vypočítať objem rôznych geometrických telies, vrátane gule, valca, kužeľa a ďalších. Tento nástroj je ideálny pre študentov, inžinierov a všetkých, ktorí potrebujú spoľahlivé výpočty objemu.

Objem kocky

Objem kvádra

Objem gule

Objem valca

Objem kužeľa

Objem ihlana

Objem hranola

Objem elipsoidu

Objem zrezaného kužeľa

Objem zrezaného ihlana

Objem torusu

Objem guľového odseku

Objem guľového výseku

Kocka

Kocka je geometrické teleso, ktorého steny tvorí šesť štvorcov. Má niekoľko vlastností:

• je špeciálnym prípadom kvádra, ktorého všetky hrany sú rovnaké,
• všetky steny kocky sú zhodné,
• každé dve protiľahlé steny kocky sú rovnobežné, 
• každé dve susedné steny sú na seba kolmé,
• každé dve hrany kocky sú rovnobežné alebo kolmé,
• kocka má 8 vrcholov,
• má 12 hrán, ktoré sú zhodné úsečky.

Objem kocky

Pod pojmom objem kocky chápeme veľkosť alebo kapacitu priestoru, ktoré kocka vypĺňa.

Objem kocky vypočítame z dĺžky jej hrán, ktorý je rovný súčinu dĺžok všetkých troch hrán, alebo jednoduchšie povedané, vypočítame ju ako tretiu mocninu dĺžky jej hrany.

Vzorec objemu kocky

V = a³

Kde: 

V = objem kocky
a = dĺžka hrany kocky

Príklad objemu kocky

Jožko si modeloval z plastelíny. Na vymodelovanie kocky s hranou dlhou 3 cm spotreboval 27g plastelíny. Koľko gramov plastelíny bude potrebovať na vymodelovanie kocky s hranou dlhou 6 cm?

Riešenie:

Použijeme vzorec objemu kocky: 

V = a³

Hrana kocky (a) predstavuje 3 cm.

V = 3³ = 27 cm³ = 27 g plastelíny.

Objem kocky s hranou dlhou 6 cm: V = 6³ = 216 cm³ = 216 g plastelíny

Výsledok: Na kocku s hranou 6 cm potrebuje Jožko 216 g plastelíny.

Kváder

Kváder je geometrické teleso, ktorého steny tvorí šesť obdĺžnikov.

Vlastnosti kvádra:

• každé dve steny kvádra sú rovnobežné alebo kolmé,
• každé dve hrany kvádra sú rovnobežné alebo kolmé,
• každé dve protiľahlé steny sú rovnobežné a zhodné.

Objem kvádra

Objem kvádra vypočítame ako súčin dĺžok jeho susedných hrán.

Vzorec objemu kvádra

V = a x b x c

Kde:

V = objem kvádra
a = dĺžka hrany
b = dĺžka hrany
c = dĺžka hrany

Príklad objemu kvádra

Ako sa zmení objem bazéna v tvare kvádra s rozmermi 2 m, 3 m a 120 cm, ak 2 m hranu zväčšíme trojnásobne a 3 m hranu dvojnásobne? 

Riešenie:

Použijeme vzorec objemu kvádra:

V = a x b x c

Pre konzistentnosť výsledku musíme do vzorca dosadiť prevedenú tretiu hranu na metre, čiže dĺžka tretej hrany bude 1,2 m.

V = 2 m x 3 m x 1,2 m = 7,2 m³

Keďže máme vyriešiť ako sa zmení objem bazéna po zväčšení hrán, tak vypočítame objem s novými dĺžkami .

V = 6 m x 6 m x 1,2 m = 43,2 m³

43,2 m³ : 7,2 m³ = 6

Výsledok: Objem pôvodného kvádra je 7,2 m³ a objem zväčšeného kvádra je 43,2 m³. Objem bazéna v tvare kvádra sa zväčší 6 krát.

Guľa

Guľa je geometrické teleso. Skladá sa z množiny bodov, ktorých vzdialenosť od pevného bodu (od stredu gule) nie je väčšia ako polomer gule.

Objem gule

Objem gule definujeme ako množstvo priestoru, ktoré táto guľa zaberá v trojrozmernom priestore.

Vzorec objemu gule

V = 4/3 x π x r³

Kde:

V = objem gule
π = “pí” matematická konštanta (Ludolfovo číslo)
r = polomer gule

Príklad objemu gule

Predstavme si, že máme basketbalovú loptu s priemerom 24 cm. Chceme zistiť aký objem priestoru táto lopta zaberá.

RIešenie:

Najprv musíme vypočítať polomer. Polomer v našom prípade je 24 cm : 2 = 12 cm.

Dosadíme hodnoty do vzorca gule:

V = 4/3 x π x r³

V = 4/3 x 3,14 x 12³

V ≈ 7234,56 cm³

Výsledok: Objem basketbalovej lopty predstavuje približne 7 234,56 cm³.

Valec

Valec, alebo aj rotačný valec, vznikne napr. otáčaním obdĺžnika okolo jeho strany. Je to geometrické teleso.

Vlastnosti valca:

• sieť valca má 2 podstavy a plášť,
• výška valca sa rovná vzdialenosti jeho podstáv,
• podstavy majú tvar kruhu.

Objem valca

Objem valca je súčin obsahu podstavy a výšky valca.

Vzorec objemu valca

V = π x r² x v

Kde:

V = objem valca
π = “pí” matematická konštanta (Ludolfovo číslo)
r = polomer valca
v = výška valca

Príklad objemu valca

Chceme postaviť detský bazén v tvare valca. Potrebujeme vypočítať koľko objemu vody sa do neho zmestí, ak vieme, že priemer podstavy je 4 metre a hĺbka 50 cm a vodu chceme naplniť po okraj.

Riešenie:

Vypočítajme najprv polomer valca. Ak priemer je 4 metre, tak polomer je 2 metre. Ďalej pre konzistentnosť výsledku premeníme 50 cm na metre, čiže 0,5 m.

Dosadíme do vzorca objemu valca:

V = π x r² x v

V = 3,14 x 2² x 0,5

V ≈ 6,28 m³

Výsledok: Do detského bazéna sa zmestí približne 6,28 m³ vody.

Kužeľ

Kužeľ (rotačný kužeľ) je geometrické teleso, ktoré vzniká otáčaním pravouhlého trojuholníka okolo jednej jeho odvesny.

Vlastnosti kužeľa:

• sieť valca má podstavu a plášť,
• výška kužeľa je vzdialenosť vrcholu kužeľa od jeho podstavy,
• podstavou kužeľa je kruh,
• plášť je časťou kruhu.

Objem kužeľa

Objem kužeľa sa rovná jednej tretine zo súčinu obsahu podstavy a výšky.

Vzorec objemu kužeľa:

V = ⅓ x π x r² x v

Kde:

V = objem kužeľa
π = “pí” matematická konštanta (Ludolfovo číslo)
r = polomer podstavy
v = výška kužeľa

Príklad objemu kužeľa

Predstavme si, že Jožko vyrába pudingové poháre v tvare kužeľa. Potrebuje zistiť, koľko pudingu sa zmestí do jedného pohára, aby vedel, koľko ho musí pripraviť. Predpokladajme, že podstava pohára má 8 cm a výška pohára je 16 cm a Jožko pudingy dáva po okraj.

Riešenie: 

Najprv si vypočítame polomer ako polovicu priemeru, tzn. polomer je 4 cm.

Dosadíme do vzorca na výpočet objemu kužeľa:

V = ⅓ x π x r² x v

V = ⅓ x 3,14 x 4² x 16

V ≈ 267,95 cm³

Výsledok: Jožko potrebuje vyrobiť 267,95 cm³ pudingu do každého pohára, čo je zároveň 267,95 mililitra.

Ihlan

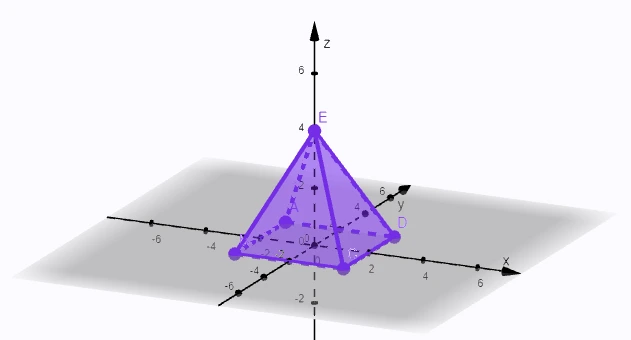
Ihlan je geometrické teleso ohraničené jedným n-uholníkom a n trojuholníkmi; n-uholník sa nazýva podstava, trojuholníky bočné steny.

Ak má ihlan n bočných stien (ak jeho podstava je n-uholník), hovoríme o n-bokom ihlane.

Trojboký ihlan nazývame štvorsten. Ak jeho podstava a ostatné steny trojbokého ihlana sú zhodné rovnostranné trojuholníky, nazývame ho pravidelný štvorsten.

Objem ihlana

Objem ihlana sa rovná jednej tretine zo súčinu jeho podstavy a dĺžky výšky.

Vlastnosti ihlana:

• sieť ihlana má jednu podstavu a plášť,
• výška ihlana je vzdialenosť vrcholu ihlana od jeho podstavy,
• podstavou môže byť trojuholník, štvorec, obdĺžnik, päťuholník, šesťuholník,…,
• ak je podstavou pravidelný útvar, získame pravidelný ihlan,
• plášť ihlana tvoria bočné steny, sú to trojuholníky.

Vzorec objemu ihlana

V = ⅓ x S_p x v

Kde:

V = Objem ihlana
S_p= obsah podstavy
v = výška ihlana

Príklad objemu ihlana

Sochár modeluje sochu v tvare ihlanu s rovnostrannou trojuholníkovou základňou. Potrebuje zistiť, koľko betónu bude potrebovať pre vyrobenie tejto sochy.

Predpokladajme, že dĺžka strany trojuholníkovej podstavy je 2 metre a výška sochy (ihlana) je 4 metre.

Riešenie:

Najprv potrebujeme vypočítať obsah podstavy. Keďže ide o rovnostranný trojuholník tak vzorec pre výpočet jeho plochy S_p je: 

S_p = √3 / 4 x a²

Kde “a” je dĺžka strany rovnostranného trojuholníka, v našom prípade 2 metre.

S_p = √3 / 4 x 2² 

S_p = √3 / 4 x 4

S_p = √3 m²

Obsah podstavy dodáme do vzorca pre výpočet objemu ihlanu.

V = ⅓ x S_p x v

V = ⅓ x √3 x 4

V = 4/3 x √3 m³

V ≈ 4/3 x 1,732 m³

V ≈ 2,309 m³

Výsledok: Sochár potrebuje vyrobiť približne 2,309 m³ betónu pre jeho sochu v tvare ihlana.

Hranol

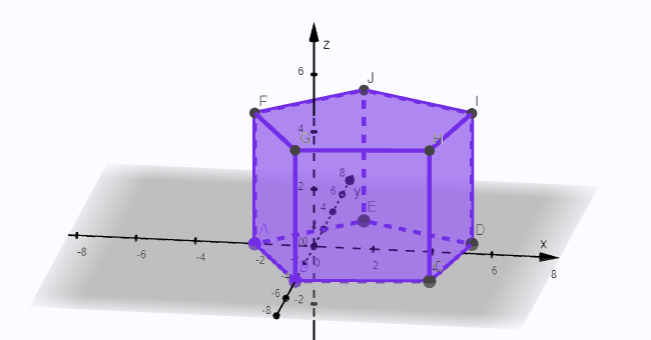
Hranol je geometrické teleso. Podstavou každého hranola je mnohouholník. Mnohouholník vždy vieme rozdeliť na neprekrývajúce trojuholníky. Hranol potom vieme rozrezať na trojboké hranoly, ktorých podstavy sú tieto trojuholníky a ich výšky sa rovnajú výške pôvodného hranola.

Objem hranola

Objem ľubovoľného hranola vypočítame tak, že vynásobíme obsah podstavy a výšku. V prípade, ak ide o iný ako trojboký hranol, tak objem hranola sa bude rovnať súčtu objemov trojbokých hranolov.

Vzorec objemu ľubovoľného hranola

V = S_p x v

Kde:

V = objem hranola
S_p = obsah podstavy 
v = výška hranola

Príklad objemu hranola

Máme akvárium, ktorého podstava je v tvare lichobežníka, kde dlhšia strana je 80 cm, kratšia strana 60 cm a výška lichobežníka je 40 cm. Ďalej vieme, že výška akvária je tiež 40 cm. Vypočítajme objem akvária (hranola s podstavou lichobežníka) a zároveň koľko vody do neho potrebujeme za predpokladu, že voda bude naplnená po okraje.

Riešenie:

Pre výpočet objemu akvária (hranola) potrebujeme zistiť obsah podstavy lichobežníka.

Vzorec pre výpočet lichobežníka je: 

S_p = ½ x (a + b) x v

Kde:

S_p = obsah lichobežníka
a = dĺžka jednej hrany
b = dĺžka druhej hrany
v = výška lichobežníka

S_p = ½ x (80 + 60) x 40

S_p – ½ x 140 x 40

S_p = 2 800 cm²

Vypočítali sme obsah podstavy lichobežníka, ktorý predstavuje 2 800 cm².

Pre výpočet objemu hranola platí:

V = S_p x v

V = 2 800 cm² x 40 cm

V = 112 000 cm³

Výsledok: Objem akvária s podstavou lichobežníka je 112 000 cm³ alebo aj 112 dm³ = 112 litrov.

Elipsoid

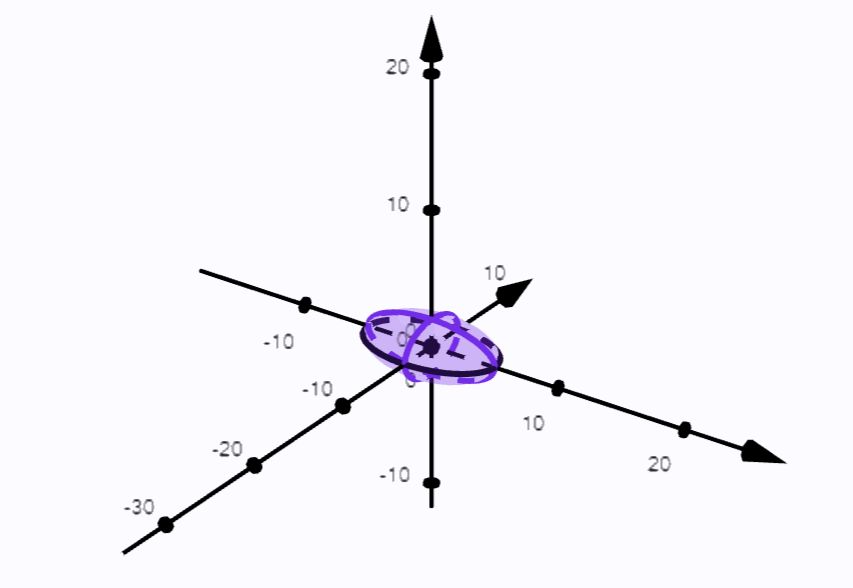
Elipsoid je geometrické teleso tvorené množinou všetkých bodov, ktorých poloha voči zadanému bodu spĺňa podmienky dané nerovnicou:

x² / a² + y² / b² + z² / c² ≤ 1

Ak by bol znak ≤ nahradený znakom =, rovnicu by spĺňali body na povrchu elipsoidu.

Objem elipsoidu

Objem elipsoidu vypočítame ako štyri tretiny súčinu Ludolfovho čísla a dĺžok hlavných a vedľajších poloosí.

Vzorec pre výpočet objemu elipsoidu

V = 4/3 x π x a x b x c

Kde:

V = objem elipsoidu
π = “pí” matematická konštanta (Ludolfovo číslo)
a, b, c = hlavné a vedľajšie poloosi

Príklad objemu elipsoidu

Predstavme si, že vyrábame elipsoidné tabletky. Každá tabletka má rozmery poloosi (dĺžka od stredu elipsoidu po jej povrch) a = 0,4 cm, b = 0,4 cm a c = 0,6 cm.

Vieme, že tabletky potrebujeme uskladniť do balenia v tvare kocky s hranou 6 cm a ďalej vieme, že maximálne môžeme vyplniť 30% priestoru balenia.

Vypočítajme koľko sa maximálne zmestí elipsoidných tabletiek do takého balenia.

Riešenie:

Najprv vypočítajme 30% z objemu kocky.

Vzorec pre výpočet objemu kocky: 

V = a³

V = 0,3 x 6³

V = 64,8 cm³

Objem elipsoidnej tablety vypočítame:

V = 4/3 x π x a x b x c

V = 4/3 x 3,14 x 0,4 x 0,4 x 0,6

V ≈ 0,10053 cm³

Ak chceme zistiť koľko sa maximálne zmestí elipsoidných tabletiek, tak to vieme vyjadriť jednoduchým vzťahom:

Počet = 30% objem kocky / objem jednej tablety

Počet = 64,8 cm³ / 0,10053 cm³

Počet ≈ 644,64

Keďže nemôžeme mať desatinný počet tabletiek, tak zaokrúhľujeme smerom nadol.

Počet = 644

Výsledok: 644 tabletiek elipsoidného tvaru môžeme uskladniť do max. 30% objemu balenia v tvare kocky s hranou 6 cm.

Zrezaný kužeľ

Zrezaný kužeľ je geometrické teleso, ktoré vzniká zrezaním kužeľa rovinou jeho vrcholu.

Výsledkom je tvar, ktorý má kruhovú podstavu pôvodného kužeľa, výšku, ktorá je kratšia ako výška pôvodného kužeľa a vrchnú podstavu má väčšinou menšiu ako spodná podstava.

Objem zrezaného kužeľa

V = ⅓ x π x v x (r²₁ + r₁ x r₂ + r²₂)

Kde:

V = objem zrezaného kužeľa
π = “pí” matematická konštanta (Ludolfovo číslo)
v = výška zrezaného kužeľa
r₁ = polomer podstavy
r₂ = polomer podstavy

Príklad objemu zrezaného kužeľa

Jožko vyrába svojpomocne nábytok. Rozhodol sa navrhnúť si stôl v tvare zrezaného kužeľa s vnútorným úložným priestorom. Šírka spodnej podstavy je 70 cm, šírka hornej podstavy je 50 cm a výška stola (zrezaného kužeľa) je 50 cm a potrebuje vypočítať objem vnútorného priestoru. Pre výpočet neuvažujeme hrúbku stien.

Riešenie:

Najprv potrebujeme upraviť šírku vrchnej a spodnej podstavy. V zadaní je udaná celková šírka, ale vzorec pre výpočet objemu zrezaného kužeľa počíta s polomerom podstáv.

Polomer spodnej podstavy = 35 cm

Polomer vrchnej podstavy = 25 cm

Dosadíme do vzorca:

V = ⅓ x π x v x (r²₁ + r₁ x r₂ + r²₂)

V = ⅓ x 3,14 x 50 x (35² + 35 x 25 + 25²)

V = ⅓ x π x 50 x (2725)

V = ⅓ x π x 136 250

V ≈ ⅓ x 3,14159 x 136 250 cm³

V ≈ 142 663,4 cm³

Výsledok: Objem vnútorného priestoru stola v tvare zrezaného kužeľa je 142 663,4 cm³, čo predstavuje približne pre predstavu 142,66 litrov priestoru.

Zrezaný ihlan

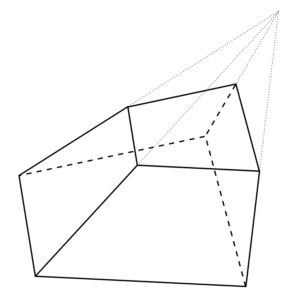
Zrezaný ihlan je geometrické teleso – časť ihlanu, ktorá leží medzi dvoma rovnobežnými rovinami prechádzajúcimi týmto ihlanom. Je to laicky povedané ihlan s odrezaným vrchom.

Zrezaný ihlan je množina všetkých bodov, ktoré získame prienikom ihlanu a rovinnej vrstvy, pokiaľ vrchol ihlanu leží vnútri vrstvy.

Objem zrezaného ihlana

Vzorec objemu zrezaného ihlana

V = ⅓ x h x (S₁ + √S₁ x √S₂ + S₂)

Kde:

V = objem zrezaného ihlana
h = vzdialenosť oboch podstáv
S₁ = obsah spodnej podstavy
S₂ = obsah vrchnej podstavy

Príklad zrezaného ihlana

Máme zrezaný štvorboký ihlan, kde:

• Dĺžka spodnej podstavy S₁ = 8 cm
• Dĺžka vrchnej podstavy S₂ = 4 cm
• Výška zrezaného ihlana je h = 10 cm

Vypočítajme objem ihlana.

Riešenie:

Najprv vypočítame obsah plochy spodnej a vrchnej podstavy. Keďže ide o ihlan so štvorcovými podstavami, tak vzorec pre výpočet je jednoduchý:

S₁ = 8²

S₂ = 4²

S₁ = 64 cm²

S₂ = 16 cm²

Použime vzorec pre výpočet objemu zrezaného ihlana:

V = ⅓ x h x (S₁ + √S₁ x √S₂ + S₂)

V = ⅓ x 10 x (64 + √64 x √16 + 16)

V = ⅓ x 10 x (64 + 8 x 4 + 16)

V = ⅓ x 10 x (64 + 32 + 16)

V = ⅓ x 10 x 112

V = ⅓ x 1120

V ≈ 373,33 cm³

Výsledok: Objem zrezaného štvorbokého ihlana je 373,33 cm³.

Torus (prstenec, anuloid)

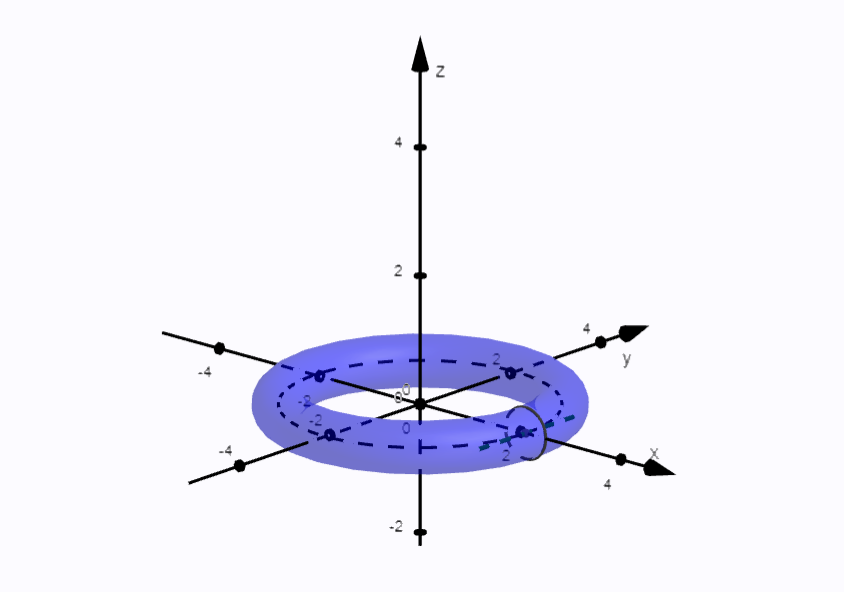
Torus (anuloid, kruhový prstenec) je teleso vytvorené rotáciou kružnice okolo priamky, ktorá leží v rovine tejto kružnice a nepretína ju. Torus si predstavme ako plávacie koleso.

Objem torusu

Vzorec pre objem torusu

V = 2 x π² x R x r²

Kde:

π = “pí” matematická konštanta (Ludolfovo číslo)
R = vzdialenosť stredu “trubice” od stredu toru
r = polomer “trubice”

Príklad objemu torusu

Vyrábame špeciálne záchranné kolesá na lode a chceme vedieť koľko vzduchu (ak nepočítame do úvahy tlak vnútri kolesa) sa do kolesa (torusu) zmestí. Predpokladajme, že vonkajší polomer (R) je 1 meter a vnútorný polomer je 0,5 metra.

Riešenie:

Dosadíme tieto hodnoty do vzorca pre výpočet objemu torusu:

V = 2 x π² x R x r²

V = 2 x 3,14² x 1 x 0,5²

V ≈ 1,2310 m³ 

Výsledok: Objem záchranného kolesa je približne 1,2310 m³.

Guľový odsek

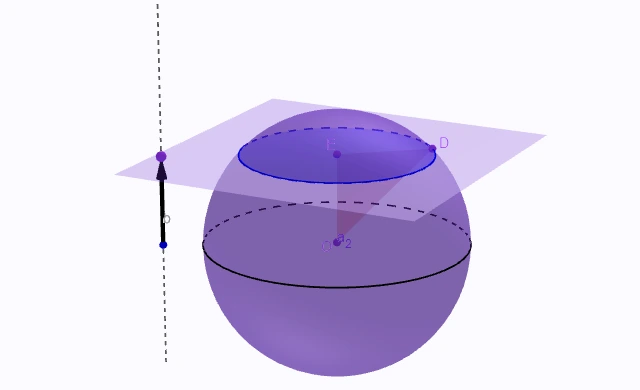
Guľový odsek je prienik gule a pol priestoru, ktorého hraničná rovina pretína guľu v kruhu s polomerom p. Tento kruh nazývame podstava guľového odseku.

Objem guľového odseku

Vzorec objemu guľového odseku

V = ⅓ x π x v² x (3 x r – v)

Kde:

V = objem guľového odseku
π = “pí” matematická konštanta (Ludolfovo číslo)
v = výška odseku
r = polomer gule

Príklad objemu guľového odseku

Predpokladajme, že máme guľový odsek s polomerom gule (R) 10 cm a výškou odseku (v) = 5 cm. Vypočítajme objem guľového odseku.

Dosadíme hodnoty do vzorca:

V = ⅓ x π x v² x (3 x r – v)

V = ⅓ x 3,14 x 5² x (3 x 10 – 5)

V = ⅓ x 3,14 x 25 x 25

V = ⅓ x 3,14 x 625

V ≈ 653,47 cm³

Výsledok: Objem guľového odseku je približne 653,47 cm³.

Guľový výsek

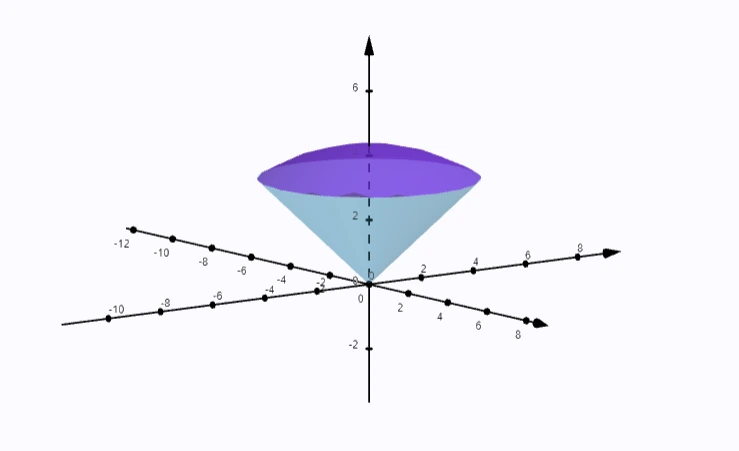
Guľový výsek vzniká zjednotením guľového odseku a rotačného kužeľa, ktorý má s guľovým odsekom spoločnú podstavu. Vrcholom rotačného kužeľa je stred gule.

Objem guľového výseku

Vzorec guľového výseku

V = ⅔ x π x r² x v

Kde:

V = objem guľového výseku
π = “pí” matematická konštanta (Ludolfovo číslo)
r = polomer gule
v = výška výseku

Príklad objemu guľového výseku

Predpokladajme, že máme guľový výsek s polomerom (r) 8 cm a výškou výseku (v) 6 cm. Vypočítajme objem guľového výseku.

Riešenie:

Dosadíme hodnoty do vzorca:

V = ⅔ x π x r² x v

V = ⅔ x 3,14 x 8² x 6

V = ⅔ x 3,14 x 64 x 6

V ≈ 804,25 cm³

Výsledok: Objem guľového výseku je približne 804,25 cm³.

Zdroje:

• DZURUSOVÁ, Anna – HLÁSNIKOVÁ, Jaroslava – KASENČÁKOVÁ, Mariana – KRAJŇÁK, Vladimír – PODPĚRA, Jan – POLÁČIKOVÁ, Katarína. Hravá matematika – Pracovný zošit pre 7. ročník ZŠ a sekundu GOŠ. 132 s. ISBN 978-80-89530-52-6
• Guľa: https://sk.wikipedia.org/wiki/Gu%C4%BEa_(matematika)
• KOLBASKÁ, Viera. Matematika pre 9. ročník základnej školy a 4. Ročník gymnázia s osemročným štúdiom. 136 s. Prvé vydanie, 2014. ISBN 978-80-10-02292-2
• ŠEDIVÝ, Ondrej – ČERETKOVÁ, Soňa – MALPEROVÁ, Mária – BÁLINT, Ľudovít. Matematika pre 9.ročník základných škôl, 2 časť. Druhé vydanie, 2004. ISBN 80-10-00397-2
• ČERETKOVÁ, Soňa – ŠEDIVÝ, Ondrej – TEPLIČKA, Ivan. Matematika pre 8. Ročník základnej školy a 3. Ročník gymnázia s osemročným štúdiom, 2. časť. 96 s. Prvé vydanie, 2023. ISBN: 978-80-10-04149-7
• Elipsoid: https://sk.wikipedia.org/wiki/Elipsoid
• Zrezaný kužeľ: https://sk.wikipedia.org/wiki/Zrezan%C3%BD_ku%C5%BEe%C4%BE
• Zrezaný ihlan: https://sk.wikipedia.org/wiki/Zrezan%C3%BD_ihlan 
• Torus: https://sk.wikipedia.org/wiki/Torus_(geometria) 
• Objem a povrch častí gule: https://www.galeje.sk/web_object/9498.pdf