Kalkulačka povrchu telies

Kalkulačka povrchu telies vypočíta plochu 13 geometrických tvarov.

Povrch kocky

Povrch kvádra

Povrch gule

Povrch valca

Povrch kužeľa

Povrch ihlanu

Povrch hranola

Povrch elipsoidu

Povrch zrezaného kužeľa

Povrch zrezaného ihlana

Povrch torusu

Povrch guľového odseku

Povrch guľového výseku

Povrch kocky

Kocka je teleso, ktorého steny tvorí šesť štvorcov. Povrch kocky predstavuje súčet obsahov všetkých jeho stien.

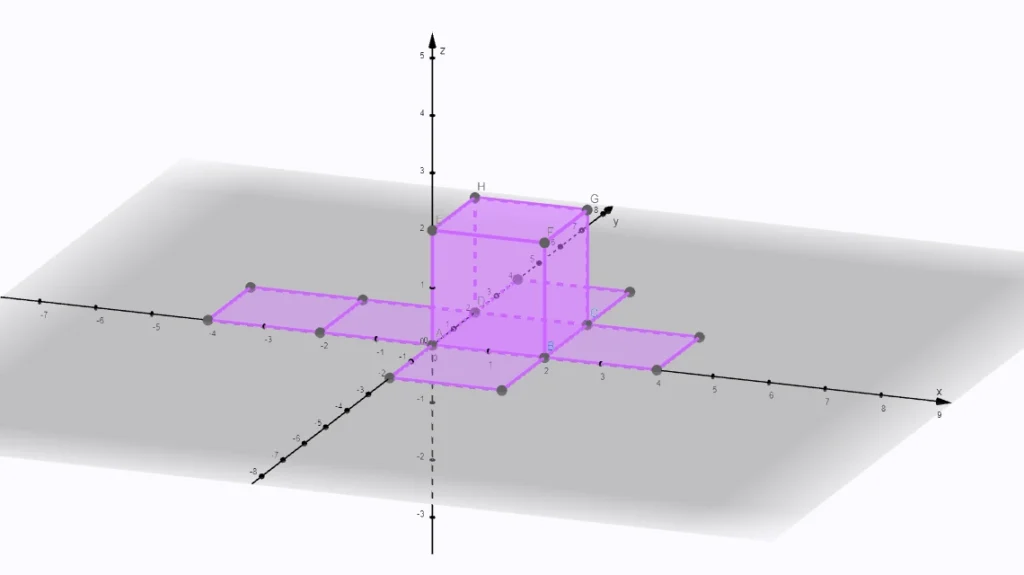
Vzorec povrchu kocky

S = 6a²

Kde:

• a = dĺžka strany.

Ak povrch kocky = 6 x obsah jednej steny kocky, potom povrch kocky s dĺžkou hrany 4 cm = 6 x 4 x 4 = 6 x 4² = 96 cm².

Využitie povrchu kocky

• ak potrebujeme zabaliť objekt tvaru kocky, tak poznaním povrchu nám pomáha určiť množstvo materiálu potrebného na jeho zabalenie,
• pri natieraní alebo pokovovaní kocky je dôležité vedieť, koľko farby, laku alebo iného materiálu spotrebujeme na pokrytie jej povrchu,
• povrch kocky môžeme spojiť s výpočtom jej objemu, čo je dôležité pri logistike, výrobe a doprave tovarov.

Povrch kvádra

Kváder je teleso, ktoré sa skladá z tých istých obdĺžnikov ako sieť kvádra.

Sieť kvádra sa skladá zo šiestich obdĺžnikov, ktorých rozmery sú určené rozmermi kvádra. Pod pojmom sieť si predstavme povrch telesa rozprestretého do roviny a vždy sa skladá z bočných stien a podstáv.

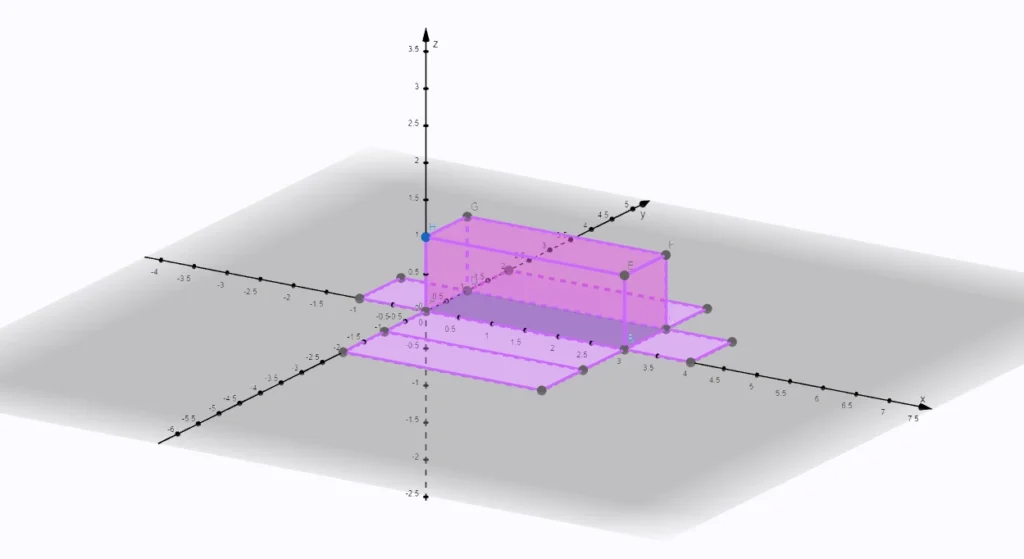
Vzorec povrchu kvádra

S = 2 x (a x b + b x c + a x c)

Kde:

• dĺžka (a), 
• šírka (b), 
• výška (c).

Povrch kvádra = 2 x obsah podstavy + 2 x obsah prednej steny + 2 x obsah bočnej steny = 2 x (obsah podstavy + obsah prednej steny + obsah bočnej steny).

Povrch kvádra s rozmermi 6 cm, 4 cm a 2 cm = 2 x 6 x 4 + 2 x 6 x 2 + 2 x 4 x 2 = 2 x (6 x 4 + 6 x 2 + 4 x 2) = 88 cm²

Využitie povrchu kvádra

Má rovnaké využitie ako v prípade kocky možno až viac univerzálnejšie, keďže kváder môže mať rozdielne dĺžky hrán.

Povrch gule

Guľa je geometrické teleso, ktoré sa skladá zo všetkých bodov priestoru X, ktoré majú od pevného bodu S (stredu gule) vzdialenosť menšiu alebo rovnajúcu sa polomeru gule r.

Guľovú plochu tvoria všetky body X priestoru, ktorých vzdialenosť od stredu S sa rovná polomeru gule |SX| = r.

Guľovú plochu nie je možné rozvinúť do roviny, teda jej sieť gule nie je možné zostrojiť.

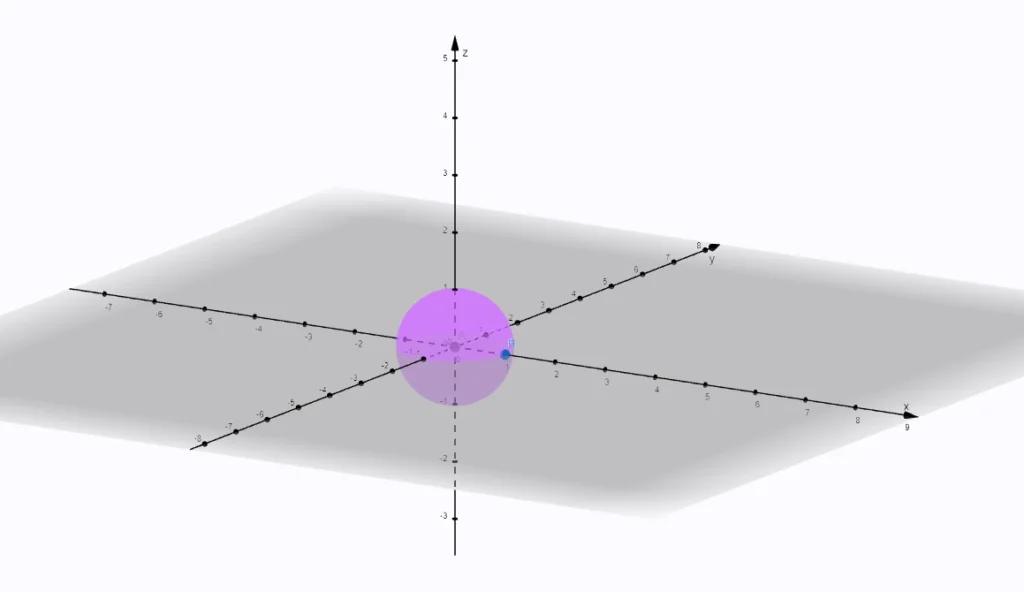
Vzorec povrchu gule

S = 4 x π x r²

Kde:

• r = polomer gule,
• π (konštanta) predstavuje pomer obvodu kruhu k jeho priemeru. Jej hodnota je približne 3,14.

Ak guľa má polomer 4 cm, tak jej obsah bude podľa vzorca: S = 4 x 3,14 x 4² = 200,96 cm².

Využitie povrchu gule

• výmena látok medzi bunkami a ich prostredím je závislá od povrchu bunky, pretože procesy, ako je difúzia, transport živín, alebo odstránenie odpadových látok, prebiehajú cez bunkovú membránu, ktorá obklopuje bunku. Veľa buniek má približne guľovitý tvar, a výpočty založené na povrchu gule poskytujú dobrý odhad plochy, cez ktorú dochádza k týmto výmenám,
• v astronómii používame výpočet povrchu planét alebo hviezd pri určení ich veľkosti,
• pri návrhu guľovitých konštrukcií vieme výpočtom povrchu určiť množstvo potrebného materiálu na ich izoláciu, nátery.

Povrch valca

Valec je geometrické teleso, ktorého podstavy sú kruhy s rovnakým polomerom.

Plášť valca tvorí obdĺžnik. Dĺžka jeho strany pri podstavách je rovná obvodu kruhovej podstavy a druhá strana obdĺžnika je výška valca.

Výška valca je vzdialenosť jeho podstáv.

Povrch valca S sa rovná súčtu obsahu dvoch podstáv a plášťa.

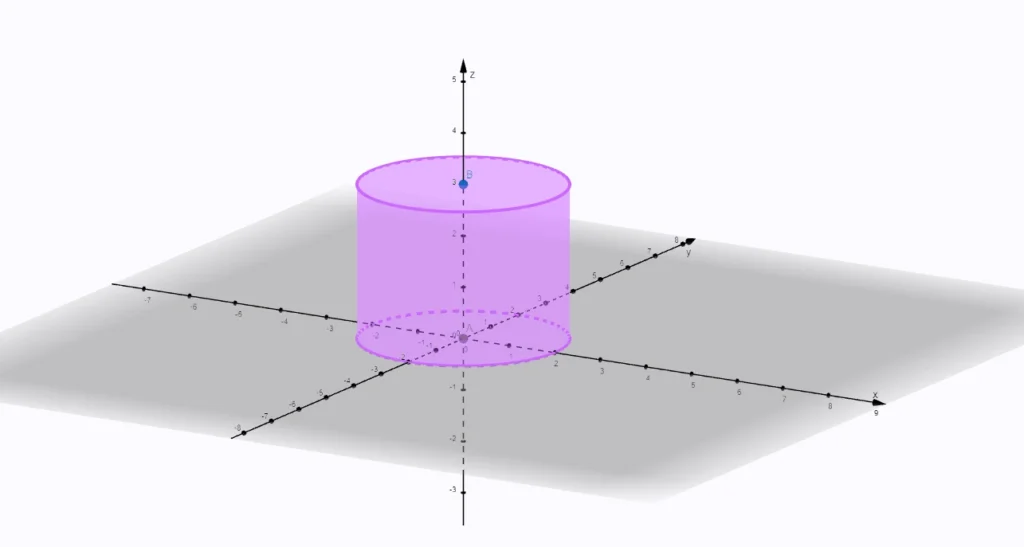
Vzorec povrchu valca

S = 2 x π x r² + 2 x π x r x v

Kde:

• polomer podstavy (r),
• výška (v),
• π (konštanta) predstavuje pomer obvodu kruhu k jeho priemeru.

Využitie povrchu valca

Mnoho vecí okolo nás má tvar valca, preto má široké použitie:

• v chemickom a potravinárskom priemysle používame valcovité nádoby na skladovanie a transport tekutín alebo sypkých materiálov. Vypočet povrchu nám umožňuje lepšie navrhnúť tepelné výmenníky alebo chladiace systémy, pretože tieto procesy závisia od veľkosti vonkajšej plochy nádoby,
• valce sú základnou súčasťou strojov (napr. piesty v motoroch),
• poznanie povrchu nám umožňuje výpočet trenia, tepelného namáhania alebo opotrebovania, ktoré súvisia s kontaktom povrchov,
• pri výpočtoch tepelného prenosu cez steny valcovitých predmetov (napr. tepelné izolácie rúr) je dôležité vedieť povrch, pretože výmena tepla závisí od veľkosti povrchu,
• pri navrhovaní valcovitých predmetov, ako sú plechovky alebo fľaše, potrebujeme poznať povrch, aby sme mohli navrhnúť etikety alebo zistiť, koľko materiálu je potrebné na ich výrobu alebo balenie.

Povrch kužeľa

Kužeľ má jednu podstavu, ktorou je kruh. Polomer podstavy označujeme r.

Každá úsečka, ktorá spája vrchol kužeľa s ľubovoľným bodom kružnice podstavy je strana kužeľa.

Všetky strany kužeľa tvoria plášť kužeľa.

Plášť kužeľa tvorí kruhový výsek.

Vzdialenosť vrcholu kužeľa od podstavy je výška kužeľa.

Povrch kužeľa S je rovný súčtu obsahu podstavy a plášťa.

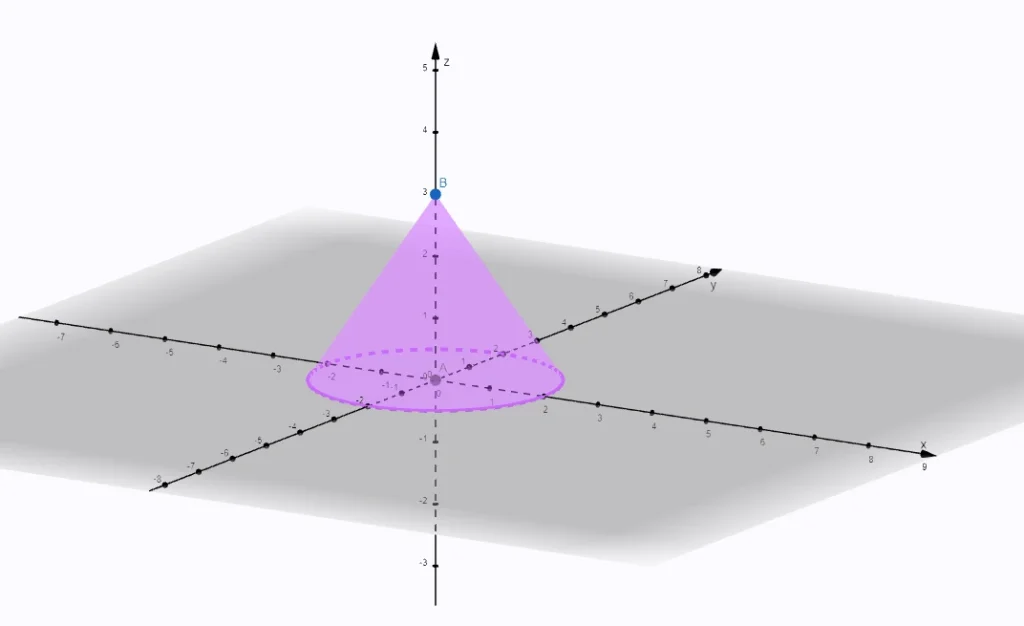
Vzorec povrchu kužeľa

S = π x r² + π x r x s

Kde:

• polomer podstavy (r), 
• výška (v), 
• strana kužeľa (s),
• π (konštanta) predstavuje pomer obvodu kruhu k jeho priemeru.

Využitie povrchu kužeľa

• v obalovom priemysle kužeľovité tvary používame na výrobu predmetov, ako sú lieviky, kornúty na zmrzlinu alebo iné nádoby. Poznanie povrchu umožňuje optimalizáciu výroby a balenia, či už ide o výpočet materiálu alebo návrh povrchových úprav,
• kužeľové tvary používame v strojoch, kde potrebujeme vypočítať povrch pre účely trenia, povrchového opotrebenia alebo kontaktu s inými časťami,
• reflektory a iné optické sústavy môžu mať kužeľovitý tvar na sústredenie alebo odrážanie svetla. Poznanie povrchu pomáha pri navrhovaní takýchto systémov na efektívne využitie odrazu svetla,
• kužeľové tvary používame v aerodynamike, napríklad pri návrhu nosových kužeľov rakiet alebo lietadiel. Povrch kužeľa potrebujeme na výpočet odporu vzduchu a na optimalizáciu tvaru, aby bolo prúdenie vzduchu čo najefektívnejšie.

Povrch ihlanu

Ihlan má jednu podstavu, ktorou môže byť trojuholník, štvoruholník, päťuholník,… Ak je podstavou pravidelný geometrický útvar (napr. štvorec, rovnostranný trojuholník), hovoríme o pravidelnom ihlane.

Plášť ihlana tvoria rovnoramenné trojuholníky.

Vzdialenosť vrcholu ihlana od podstavy je výška ihlana.

Povrch ihlana S sa rovná súčtu obsahu podstavy a plášťa.

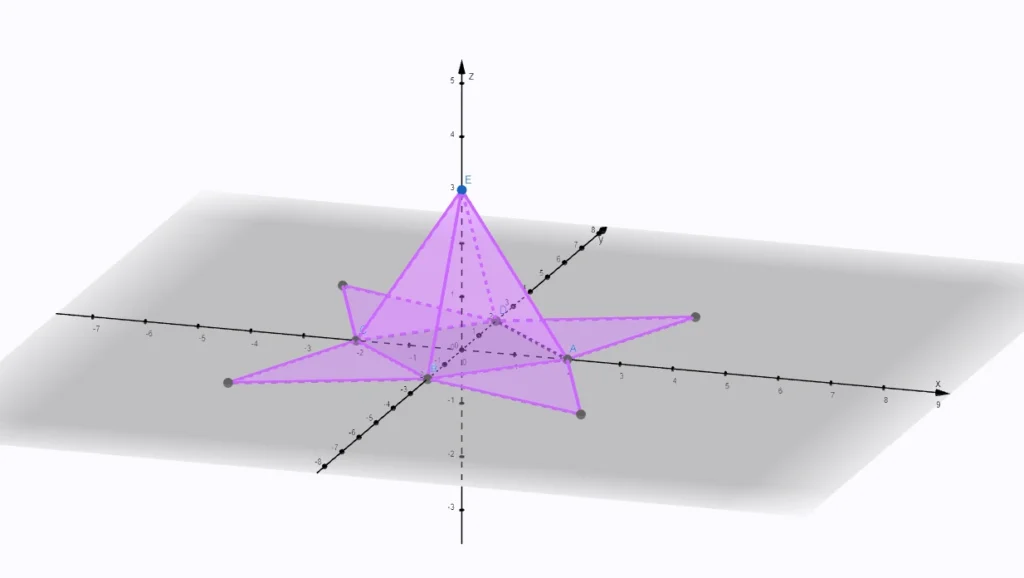
Vzorec povrchu ihlana

S = Sp + Spl

Kde:

• obsah podstavy (Sp), 
• obsah plášťa (Spl).

Využitie povrchu ihlana

• ihlanovité tvary používame pri návrhu striech, veží. Povrch ihlana potrebujeme pre určenie množstva materiálu potrebného na ich konštrukciu alebo pokrytie (napríklad škridlami či plechom),
• v technických projektoch, kde pracujeme s rôznymi tvarmi (napr. kužeľovité alebo ihlanovité súčiastky), je dôležité vedieť povrch na určenie kontaktu s inými povrchmi, trenia alebo potrebného materiálu,
• ihlanovité reflektory alebo iné konštrukcie s kužeľovým alebo ihlanovým tvarom používame na sústredenie svetla alebo tepla. Výpočet povrchu pomáha optimalizovať tieto zariadenia.

Povrch hranola

Povrch hranola je súčet plôch všetkých jeho stien. Hranol má dve základne, ktoré sú zhodné, a bočné steny, ktoré spájajú tieto základne.

Povrch hranola sa preto skladá z povrchu základní a povrchu bočných stien, alebo obsahu plášťa.

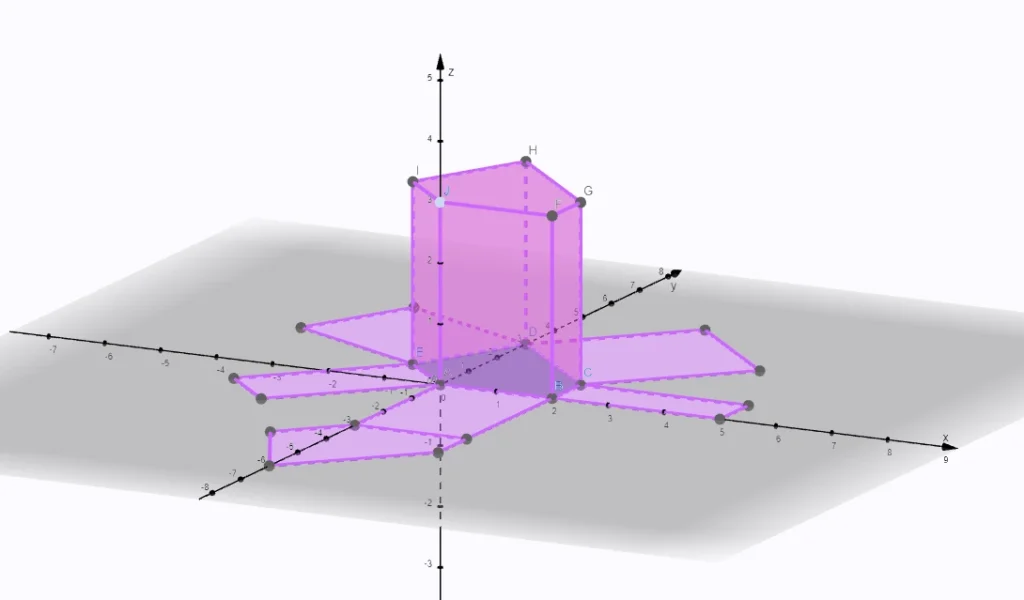
Typy hranolov

• pravidelný hranol: má základne, ktoré sú pravidelnými mnohouholníkmi (napr. štvorcový hranol, trojuholníkový hranol). V takýchto prípadoch sa výpočet povrchu môže líšiť podľa tvaru základne,
• nepravidelný hranol: základné sú nepravidelné mnohouholníky (napr. pravouhlý trojuholník, rovnoramenný trojuholník, obdĺžnik, lichobežník,…).

Vzorec povrchu hranola

S = 2 x Sp + Spl

Kde:

• obsah podstavy (Sp), 
• obsah plášťa (Spl).

Využitie povrchu hranola

• hranolovité tvary využívame v konštrukciách, ako sú budovy, stĺpy, mosty a nádrže. Povrch hranola umožňuje výpočet množstva materiálu potrebného na pokrytie izolácie, fasády, náterov alebo iných povrchových úprav,
• hranolovité nádoby a obaly používame v mnohých priemyselných odvetviach. Ak vieme povrch, tak vieme určiť koľko materiálu potrebujeme na výrobu obalu (napríklad krabíc) alebo na návrh etikiet,
• výpočet povrchu potrebujeme pre správne pokrytie povrchu nábytku, napr. lamináciou alebo farbením a na určenie množstva materiálu potrebného na jeho výrobu.

Povrch elipsoidu

Povrch elipsoidu je celková plocha jeho trojrozmernej, oválnej (eliptickej formy).

Elipsoid je tvar, ktorý vzniká rotáciou okolo jednej z jej osí.

Na rozdiel od gule, ktorá má rovnaký polomer vo všetkých smeroch; elipsoid má tri rôzne polomery, ktoré predstavujú jeho osi.

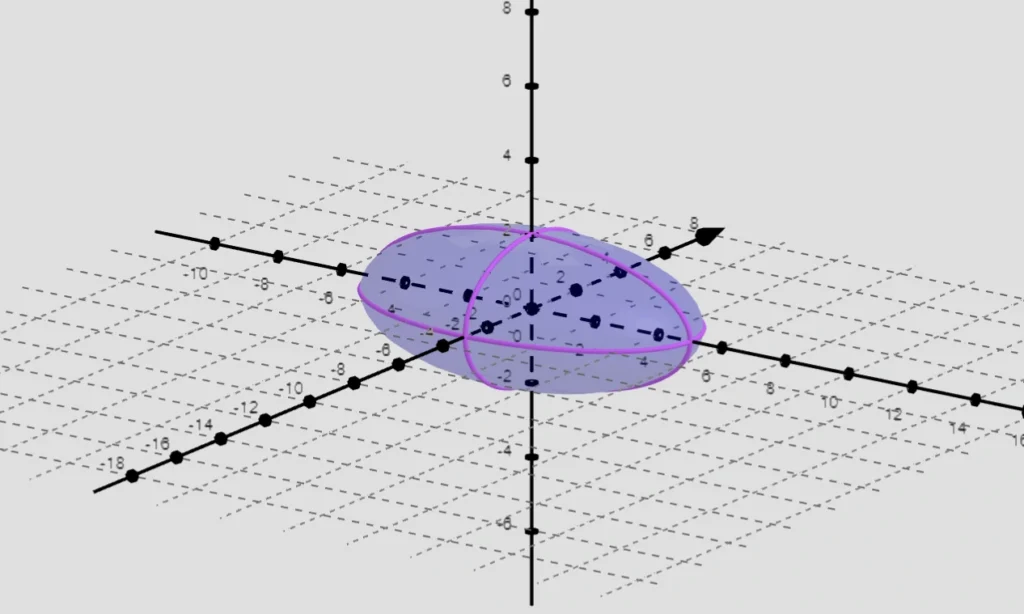
Vzorec povrchu elipsoidu

S ≈ 4 x π x ((a^p x b^p + a^p x c^p + b^p x c^p) /3) ^1/p

Kde:

• p = konštanta 1,6075
• polomer osi x (a), 
• polomer osi x (b), 
• polomer osi z (c),
• π (konštanta) predstavuje pomer obvodu kruhu k jeho priemeru.

Využitie povrchu elipsoidu

• systémy GPS a ďalšie navigačné technológie pracujú s elipsoidným modelom Zeme na presné určenie polohy a vzdialeností,
• pri skúmaní mesiacov alebo asteroidov s nepravidelnými tvarmi sa môžu použiť elipsoidné modely na odhady ich povrchových rozmerov,
• elipsoidné tvary používame pri návrhu šošoviek a optických zariadení, pretože majú špecifické vlastnosti zamerané na ohýbanie svetla. Povrchové výpočty nám pomáhajú navrhovať presné komponenty v optických systémoch – v teleskopoch alebo v mikroskopoch.

Povrch zrezaného kužeľa

Povrch zrezaného kužeľa sa skladá z dvoch základní (hornej a dolnej kruhovej plochy) a bočnej plochy (plášťa), ktorá spája tieto základne.

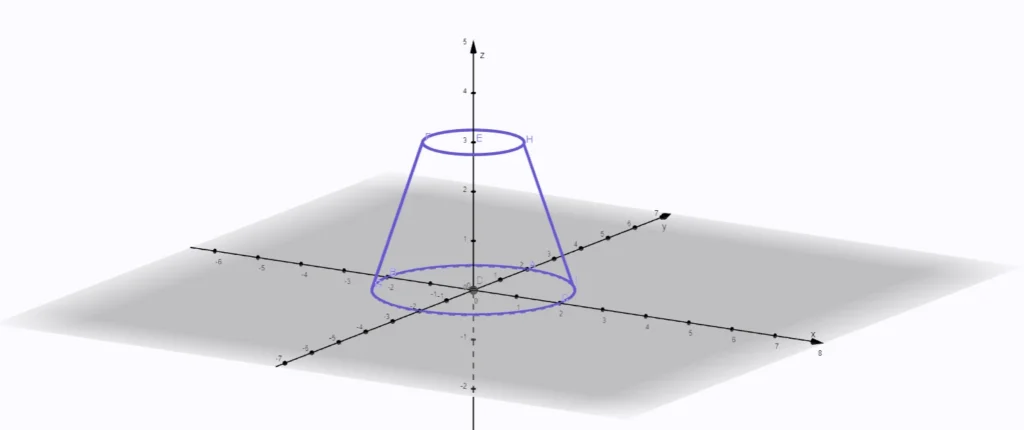
Vzorec zrezaného kužeľa

S = π x r1² + π x r2² + π x (r1 +r2) x odmocnina z (v² + (r1 – r2)²)

Kde:

• polomer dolnej podstavy (r1), 
• polomer hornej podstavy (r2), 
• výška (v),
• π (konštanta) predstavuje pomer obvodu kruhu k jeho priemeru.

Využitie povrchu zrezaného kužeľa

• v priemysle balenia môžu mať niektoré nádoby tvar zrezaného kužeľa. Poznanie povrchu pomáha pri výpočte množstva materiálu potrebného na výrobu obalu,
• zrezané kužele používame v návrhoch reflektorov alebo tepelných zariadení, kde je dôležitá plocha plášťa pre odraz alebo prenos tepla,
• zrezané kužele používame pri dizajne objektov ako poháre, nádrže alebo komíny, kde potrebujeme vypočítať povrch pre efektívnu výrobu.

Povrch zrezaného ihlana

Povrch zrezaného ihlana pozostáva z viacerých častí: základní (dolnej a hornej) a bočných plôch (stien). Zrezaný ihlan je trojrozmerný tvar, ktorý vznikne odstránením vrchnej časti ihlanu (napríklad „orezaním“ jeho vrcholu).

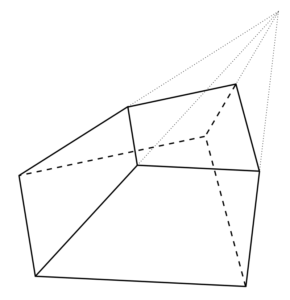
Vzorec povrchu zrezaného ihlanu

S = Sp1 + Sp2 + Spl

Kde:

• plocha dolnej podstavy (Sp1), 
• plocha hornej podstavy (Sp2), 
• plocha plášťa (Spl).

Využitie povrchu zrezaného ihlana

• priemyselné komponenty (filtre alebo rozdeľovače), môžu mať tvar zrezaného ihlana. Presné výpočty povrchu potrebujeme pre efektívny návrh dizajnu,
• pri skúmaní mechanických vlastností materiálov môžeme zrezané ihlany využívať na analýzu správania sa materiálov pri rôznych podmienkach,
• zrezané ihlany používame na návrh nádrží a síl.

Povrch torusu

Povrch torusu je geometrický pojem, ktorý opisuje plochu tvaru, ktorý pripomína donut alebo krúžok. Torus sa vytvára rotáciou kruhu okolo osi, ktorá neleží v rovine tohto kruhu.

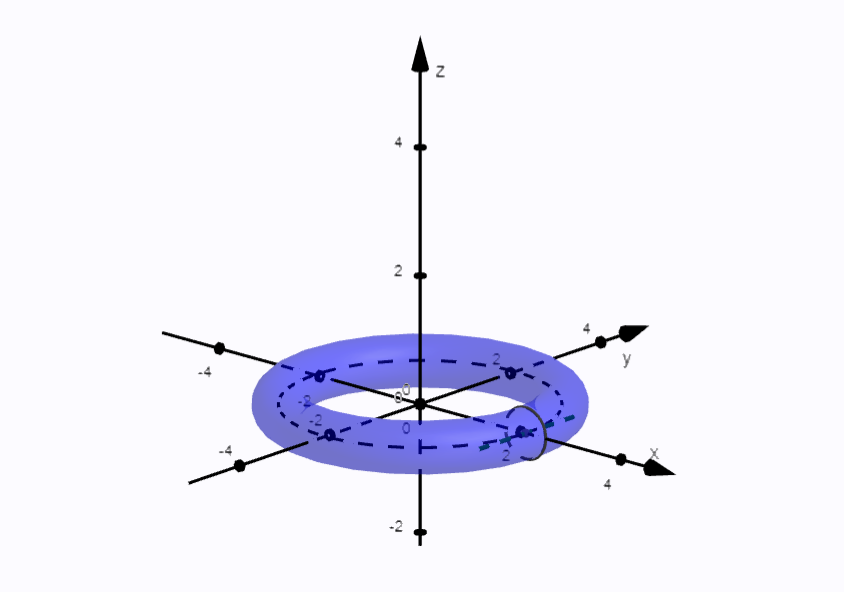
Vzorec povrchu torusu

S = (2 x π x r) x (2 π x R)

Kde:

• polomer kružnice stredu torusu R,
• polomer trubice r,
• π (konštanta) predstavuje pomer obvodu kruhu k jeho priemeru.

Využitie povrchu torusu

• ložiská alebo tesnenia môžu mať torusové tvary. Poznanie povrchu je preto dôležité pre stanovenie správnych tolerancií a rozmerov,
• torusy sa často používame na návrh nádrží a potrubí, kde tvar ovplyvňuje prúdenie kvapalín a plynov. Presný výpočet povrchu pomáha pri optimalizácii dizajnu a materiálov.

Povrch guľového odseku

Povrch guľového odseku je plocha, ktorá vzniká pri rezaní gule rovinou, ktorá prechádza guľou.

Guľový odsek môže byť považovaný za časť gule, ktorá je „odrezaná“ od zvyšku gule a má tvar, ktorý je kombináciou guľovej plochy a základne.

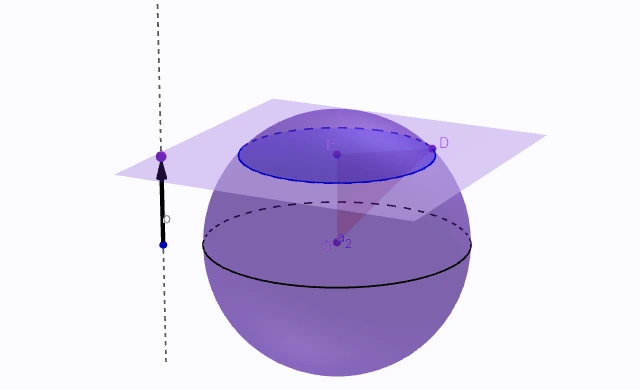
Vzorec pre povrch guľového odseku

S = π x (q² + 2 x r x v)

Kde:

• polomer gule (r), 
• výška odseku (h), 
• priemer podstavy (q),
• π (konštanta) predstavuje pomer obvodu kruhu k jeho priemeru.

Využitie povrchu guľového odseku

• guľové odseky používame pri navrhovaní kupolových štruktúr, ako sú kostoly, pavilóny a iné budovy, kde je zakrivený tvar esteticky atraktívny a zároveň funkčný,
• v oblasti fyziky a mechaniky môže byť guľový odsek použiť na modelovanie prúdenia tekutín v zakrivených priestoroch,
• guľové odseky môžu byť použité ako vzdelávacie pomôcky na vizualizáciu geometrických a fyzikálnych konceptov.

Povrch guľového výseku

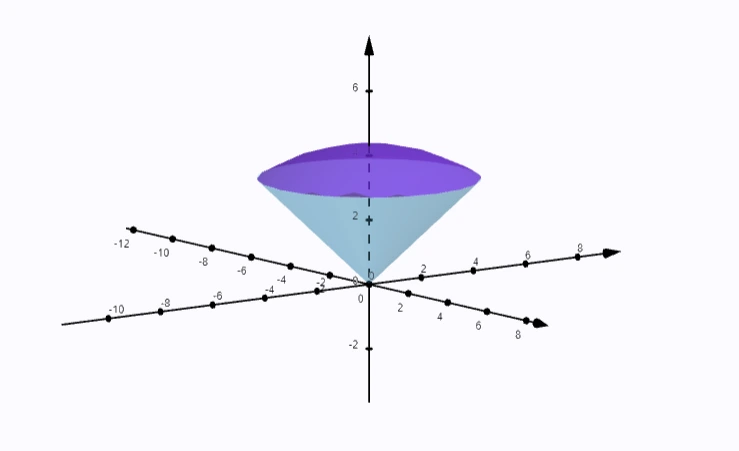
Povrch guľového výseku je plocha, ktorá vzniká pri rezaní gule rovinou, ktorá prechádza guľou. Guľový výsek predstavuje časť povrchu gule a je definovaný tromi hlavnými prvkami:

• guľová časť: zakrivená plocha, ktorá je časťou povrchu gule,
• základňa: rovinná plocha, ktorá vzniká pri reze guľou a má tvar kruhu,
• výška: vzdialenosť medzi základňou a najvyšším bodom guľového výseku.

Vzorec guľového výseku

S = π x r (r + 2 x v)

Kde:

• polomer gule (r), 
• výška výseku (v),
• π (konštanta) predstavuje pomer obvodu kruhu k jeho priemeru.

Využitie guľového výseku

• V raketových motoroch alebo vesmírnych zariadeniach vyrábame nádrže na palivo ako časti gule (guľové výseky) kvôli optimalizácii tlaku a rozloženiu síl. Vypočítanie povrchu potrebujeme na presný návrh stien nádrže, ich hrúbky a materiálových požiadaviek (napríklad na povrchovú ochranu proti korózii),
• parabolické satelity a antény majú tvar podobný guľovému výseku. Vypočítanie povrchu tejto časti je kľúčové pri návrhu materiálu, jeho pokrytia (napríklad vodivou vrstvou alebo ochranným náterom), a na správne rozloženie signálov,
• implantáty v ortopedickej chirurgii (náhrady kĺbov) môžu mať tvar guľových výsekov. Výpočet povrchu umožňuje presnejší návrh implantátu a určuje jeho povrchovú úpravu (napríklad titánový náter na ochranu pred koróziou).

Zdroje:

• DZURUSOVÁ, Anna – HLÁSNIKOVÁ, Jaroslava – KASENČÁKOVÁ, Mariana – KRAJŇÁK, Vladimír – PODPĚRA, Jan – POLÁČIKOVÁ, Katarína. Hravá matematika – Pracovný zošit pre 7. ročník ZŠ a sekundu GOŠ. 132 s. ISBN 978-80-89530-52-6
• KOLBASKÁ, Viera. Matematika pre 9. ročník základnej školy a 4. Ročník gymnázia s osemročným štúdiom. 136 s. Prvé vydanie, 2014. ISBN 978-80-10-02292-2
• ČERETKOVÁ, Soňa – ŠEDIVÝ, Ondrej – TEPLIČKA, Ivan. Matematika pre 8. Ročník základnej školy a 3. Ročník gymnázia s osemročným štúdiom, 2. časť. 96 s. Prvé vydanie, 2023. ISBN: 978-80-10-04149-7
• ŽABKA, Ján – ČERNEK, Pavol. Matematika pre 8. ročník ZŠ a 3. ročník gymnázií s osemročným štúdiom. 143 s. ISBN 978-80-8120-125-7
• ŠEDIVÝ, Ondrej – ČERETKOVÁ, Soňa – MALPEROVÁ, Mária – BÁLINT, Ľudovít. Matematika pre 9.ročník základných škôl, 2 časť. Druhé vydanie, 2004. ISBN 80-10-00397-2
• Objem a povrch častí gule: https://www.galeje.sk/web_object/9498.pdf
• Elipsoid: https://sk.wikipedia.org/wiki/Elipsoid
• Zrezaný kužeľ: https://sk.wikipedia.org/wiki/Zrezan%C3%BD_ku%C5%BEe%C4%BE
• Zrezaný ihlan: https://sk.wikipedia.org/wiki/Zrezan%C3%BD_ihlan 
• Torus: https://sk.wikipedia.org/wiki/Torus_(geometria)