Mocniny a odmocniny (kalkulačka)

Kalkulačka mocniny vypočíta hodnotu čísla umocneného na daný exponent a kalkulačka odmocniny vypočíta číslo, ktoré po umocnení na daný stupeň vypočíta pôvodné číslo.

Kalkulačka mocniny

x=   y= 

Kalkulačka odmocniny

x=   y= 

Mocniny

Prestavme si, že máme vypočítať obsah štvorca. Vzorec je:

S = a2 alebo aj ako a x a

Kde:

„a2“ nazývame druhá mocnina čísla a. Čítame „a na druhú„. Hovoríme, že „umocňujeme číslo a na druhú„.

Číslo „a“ v mocninách (napr. a2) nazývame základ mocniny. Čísla 1,2,3,… 10, … (napr. a2) nazývame mocniteľ alebo exponent mocniny.

Ak by sme mali vypočítať objem kocky, tak vzorec je a3 alebo aj ako a x a x a.

„a3“ nazývame tretia mocnina čísla a. Čítame „a na tretiu„. Hovoríme, že „umocňujeme číslo a na tretiu“ atď.

Druhé mocniny opačných čísel sa rovnajú. Platí a2 = (-a)2. Čísla a, -a sú opačné čísla.

  • Párna mocnina kladného aj záporného čísla je vždy kladné číslo, napr. 22 alebo (-2)2 = 4
  • Nepárna mocnina kladného čísla je vždy kladné číslo, napr. 23 = 8.
  • Nepárna mocnina záporného čísla je vždy záporné číslo, napr. (-2)3 = -8.

Čísla, ktoré čítame rovnako zľava aj sprava, voláme palindrómy. Príklad:

  • 12 = 1
  • 112 = 121
  • 1112 = 12321
  • 11112 = 1234321

Platí, že nultá mocnina nuly je stále nula, tzn. 00 = 0, ale akékoľvek nenulové číslo na nultú je 1, napr. 30 = 1.

Mocnina s prirodzeným mocniteľom je výraz an.

  • a je základ mocniny, n je mocniteľ (exponent) mocniny, a môže byť ľubovoľné číslo,
  • n je prirodzené číslo, takže môže byť 1,2,3,4,… Čítame ako „a na en-tú„.

Odmocniny

Každá počtová operácia má v matematike svoju opačnú operáciu. Preto opakom mocniny je odmocnina a opakom umocňovania je odmocňovanie.

Ak vieme, že záhrada má plochu 100 m2 a má tvar štvorca, tak akú dĺžku má táto záhrada?

Riešenie:

Obsah štvorca je a x a, alebo aj a2. Ak vieme, že S = a2, tak a2 = 100 a tým pádom a = √100 = 10. Odpoveďou by bolo, že záhrada má dĺžku 10 metrov.

Hovoríme, že druhá odmocnina z a je také číslo b, ktorého druhá mocnina je a.

Zapísané stručnejšie a matematicky: √a = b práve vtedy, keď b2 = a pre a>= 0, b>=0.

  • √ = znak odmocnenia (v našom prípade druhá odmocnina)
  • a = základ odmocniny (odmocnenec)
  • b = výsledok odmocnenia

Podobne hovoríme, že tretia odmocnia z a je také číslo b, ktorého tretia mocnina je a.

Zapísané stručnejšie a matematicky: ∛a = b práve vtedy, keď b3 = a.

  • ∛ = znak odmocnenia (v našom prípade tretia odmocnina)
  • a = základ odmocniny (odmocnenec)
  • b = výsledok odmocnenia

Platí, že:

  • √0 = 0,
  • √1 = 1,
  • ∛0 = 0,
  • ∛1 = 1.

Graf mocnín a odmocnín

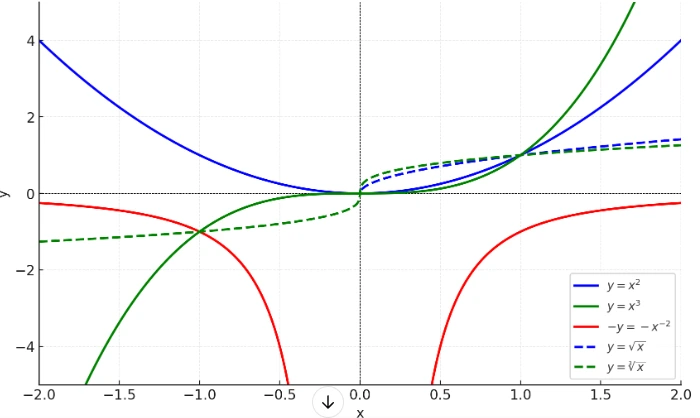
Graf mocnín a inverzných funkcií k mocninám (odmocniny). Zdroj: Vlastné spracovanie.

Na obrázku vyššie vidíme funkcie (mocniny prezentované plnou čiarou) a k nim inverzné funkcie (odmocniny).

Funkcia – y = – x-2 nemá inverznú funkciu, pretože:

  • je symetrická iba v jednej časti svojho definičného oboru (len pre kladné alebo len pre záporné x).
  • na to, aby funkcia mala inverznú funkciu, musí byť jednoznačná (y nesmie mať dve rôzne hodnoty pre jedno x), čo v našom prípade neplatí.

Všimnime si, že modrá prerušovaná čiara (y = √x) nám chýba v ľavom hornom kvadrante, pretože funkciu definujeme iba pre x ≥ 0. V reálnych číslach nie je odmocnina zo záporného čísla definovaná (iba v komplexných číslach).

Zdroje: