Obsah kruhu (kalkulačka)

Kalkulačka obsahu kruhu umožňuje vypočítať plochu kruhu rôznymi spôsobmi – v závislosti od toho, aké údaje poznáme. Využíva matematické vzorce na základe geometrických vlastností kruhu a dokáže prispôsobiť výpočet podľa zadaného vstupu.

Obsah kruhu, ak poznáme polomer (r)

Obsah kruhu, ak poznáme priemer kruhu (d)

Obsah kruhu ak poznáme obvod kruhu (o)

Obsah kruhu ak poznáme dĺžku uhlopriečky obdĺžnika, ktorému je kruh opísaný

Obsah kruhu, ak poznáme obsah štvorca, do ktorého je kruh vpísaný

Obsah kruhu, ak poznáme súradnice stredu a bodu na kružnici

Okrem výpočtu obsahu kruhu si môžete pozrieť aj naše kalkulačky na obsah štvorca, obsah obdĺžnika či obsah lichobežníka, ktoré vám pomôžu s výpočtami jednoduchších geometrických tvarov.

Ako vypočítať obsah kruhu, ak poznáme polomer (r)

zadáme dĺžku polomeru kruhu (r) napr. v centimetroch alebo iných jednotkách,
uistime sa, že polomer je väčší ako 0,
klikneme na tlačidlo „Vypočítať“,
kalkulačka zobrazí výsledok obsahu kruhu v štvorcových jednotkách.

Vzorec obsahu kruhu, ak poznáme polomer (r)

S = π * r²

Kde:

S je plocha kruhu,
π je matematická konštanta, ktorá vyjadruje pomer obvodu kruhu k jeho priemeru. π ≈ 3,14,
r je polomer kruhu.

Príklad výpočtu obsahu kruhu, ak poznáme polomer (r)

Máme kruh s priemerom d = 10 cm. Aký je jeho obsah?

Riešenie:

Najprv musíme vypočítať polomer z priemeru. Z matematiky už vieme, že polomer (r) = priemer (d) / 2. Teda polomer (r) v našom príklade je 5 cm.

Použijeme vzorec:

S = π * r² = 3,14 *5² = 3,14 * 25 = 78,5

Výsledok: Obsah kruhu je 78,5 cm².

Ako vypočítať obsah kruhu, ak poznáme priemer kruhu (d)

zadáme dĺžku priemeru kruhu (d) napr. v centimetroch alebo iných jednotkách,
uistime sa, že priemer je väčší ako 0,
klikneme na tlačidlo „Vypočítať“,
kalkulačka zobrazí výsledok obsahu kruhu v štvorcových jednotkách.

Vzorec obsahu kruhu, ak poznáme priemer (d)

S = π * (d / 2)² = π * d² / 4

Kde:

S je plocha kruhu,
π je matematická konštanta, ktorá vyjadruje pomer obvodu kruhu k jeho priemeru. π ≈ 3,14,
d je priemer kruhu.

Príklad výpočtu obsahu kruhu, ak poznáme priemer (d)

Overíme správnosť výsledku z predchádzajúceho príkladu, ak ponecháme priemer kruhu (d) s dĺžkou 10 cm.

Riešenie:

Použijeme upravený vzorec pre výpočet, ak je zadaný priemer kruhu (d).

S = (π * d²) / 4 = (3,14 *10²) / 4 = 314 / 4 = 78,5.

Výsledok: Obsah kruhu, ak poznáme jeho priemer (d), je 78,5 cm².

Ako vypočítať obsah kruhu, ak poznáme obvod kruhu (o)

zadáme dĺžku obvodu kruhu (o) – napríklad v centimetroch alebo metroch,
uistime sa, že zadaná hodnota je väčšia ako 0,
kliknite na tlačidlo „Vypočítať“,
kalkulačka automaticky zobrazí obsah kruhu v štvorcových jednotkách.

Vzorec obsahu kruhu, ak poznáme obvod kruhu (o)

S = o² / 4π

Kde:

S je plocha kruhu,
o je obvod kruhu,
π je matematická konštanta, ktorá vyjadruje pomer obvodu kruhu k jeho priemeru. π ≈ 3,14.

Príklad výpočtu obsahu kruhu, ak poznáme obvod (o)

Povedzme, že máme kruh, ktorého obvod (o) je 6 metrov a chceme vypočítať jeho plochu.

Riešenie:

Hodnotu obvodu kruhu dosadíme do vzorca:

S = o² / 4π = 6² / 4 * 3,14 = 36 / 12,56 ≈ 2,886

Výsledok: Obsah kruhu, ak je jeho obvod 6 metrov, je približne 2,886 m².

Ako vypočítať obsah kruhu, ak poznáme dĺžku uhlopriečky (d) obdĺžnika, ktorému je kruh opísaný

zadáme dĺžku uhlopriečky (d) obdĺžnika, do ktorého je kruh opísaný – napríklad v milimetroch, centimetroch alebo metroch,
uistime sa, že zadaná hodnota je väčšia ako 0,
kliknite na tlačidlo „Vypočítať“,
kalkulačka automaticky zobrazí obsah kruhu v štvorcových jednotkách.

Vzorec obsahu kruhu, ak poznáme dĺžku uhlopriečky (d) obdĺžnika, ktorému je kruh opísaný

Na výpočet obsahu použijeme 2 vzorce, kedy najprv zistíme polomer, aby sme mohli vypočítať samotný obsah kruhu.

r = d / 2

Kde:

r je polomer,
d je dĺžka uhlopriečky v obdĺžniku.

Po výpočte dĺžky polomeru, dosadíme do klasického vzorca:

S = π * r²

Kde:

S je plocha kruhu,
π je matematická konštanta, ktorá vyjadruje pomer obvodu kruhu k jeho priemeru. π ≈ 3,14,
r je polomer kruhu.

Príklad výpočtu obsahu kruhu, ak poznáme dĺžku uhlopriečky (d) obdĺžnika ktorému je kruh opísaný

Máme obdĺžnik, do ktorého je opísaný kruh, a poznáme dĺžku uhlopriečky tohto obdĺžnika: d = 10 cm. Aký je obsah opísaného kruhu?

Riešenie:

Zistíme polomer kruhu – ten je rovný polovicu uhlopriečky, čiže: r = d / 2 = 10 / 2 = 5 cm

Použijeme klasický vzorec pre obsah, ak poznáme polomer:

S = π * r² = 3,14 * 5² = 3,14 * 25 = 78,5

Výsledok: Obsah kruhu, opísaného obdĺžniku so známou dĺžkou uhlopriečky, je 78,5 cm².

Ako vypočítať obsah kruhu, ak poznáme obsah štvorca, ktorému je kruh vpísaný

zadáme obsah štvorca v jednotkách „na druhú“,
klikneme na tlačidlo „Vypočítať“,
kalkulačka vypočíta obsah vpísaného kruhu vo štvorci.

Vzorec obsahu kruhu, ak poznáme obsah štvorca, ktorému je kruh vpísaný

Ak máme zadaný obsah štvorca, tak najprv potrebujeme zistiť dĺžku jeho strany (a):

strana a =√S

Kde:

strana a je strana štvorca,
S je obsah štvorca.

Následne používame vzorec pre výpočet polomeru (r):

r = a / 2

Kde:

r je polomer kruhu,
a je strana štvorca.

Ak poznáme polomer (r), vieme tento údaj vložiť do klasického vzorca pre výpočet obsahu kruhu:

S = π * r²

Kde:

S je plocha kruhu,
π je matematická konštanta, ktorá vyjadruje pomer obvodu kruhu k jeho priemeru. π ≈ 3,14,
r je polomer kruhu.

Príklad výpočtu obsahu kruhu, ak poznáme obsah štvorca ktorému je kruh vpísaný

Máme štvorec s obsahom S = 64 cm². Do štvorca je vpísaný kruh. Aký je obsah tohto kruhu?

Riešenie:

Vypočítame dĺžku strany štvorca pomocou vzorca:

strana a =√S = √64 = 8 cm.

Následne polomer kruhu je polovica strany štvorca?

r = a / 2 = 8 / 2 = 4 cm

Obsah kruhu vypočítame dosadením polomeru do klasického vzorca:

S = π * r² = 3,14 * 4² = 3,14 * 16 ≈ 50,24

Výsledok: Obsah vpísaného kruhu vo štvorci je približne 50,24 cm².

Ako vypočítať obsah kruhu, ak poznáme súradnice stredu a bodu na kružnici (geometrický prístup)

Zadáme:

x-ovú súradnicu stredu kruhu (napr. 3,5),
y-ovú súradnicu stredu kruhu (napr. -2,0),
x-ovú súradnicu bodu na kružnici (napr. 7,0),
y-ovú súradnicu bodu na kružnicu (napr. 1,5),
klikneme na tlačidlo „Vypočítať“,
kalkulačka vypočíta obsah kruhu podľa súradníc stredu a bodu na kružnici.

Vzorec obsahu kruhu, ak poznáme súradnice stredu a bodu na kružnici (geometrický prístup)

Potrebujeme vypočítať polomer kruhu zo súradníc použitím vzorca:

r = √[(x₂ − x₁)² + (y₂ − y₁)²]

Kde:

x₁, y₁ sú súradnice stredu kruhu,
x₂, y₂ sú súradnice ľubovoľného bodu na obvode kruhu.

Ak poznáme polomer r, vieme ho použiť do klasického vzorca pre výpočet:

S = π * r²

Kde:

S je plocha kruhu,
π je matematická konštanta, ktorá vyjadruje pomer obvodu kruhu k jeho priemeru. π ≈ 3,14,
r je polomer kruhu.

Príklad výpočtu obsahu kruhu, ak poznáme súradnice stredu a bodu na kružnici (geometrický prístup)

Máme kruh, kde poznáme nasledujúce údaje:

Stred kruhu má súradnice x ₁ (3,5) a y₁ (-2,0),
bod na kružnici mú súradnice x₂ (7,0) a y₂ (1,5).

Vypočítajme obsah kruhu.

Riešenie:

Vzorec pre výpočet polomeru (r):

r = √[(x₂ − x₁)² + (y₂ − y₁)²] = √ [(7,0 – 3,5)² + (1,5 – (-2,0))²] = √ [(3,5)² + (3,5)²] = √ [12,25 + 12,25] = √24,5 ≈ 4,95

Máme polomer (r), ktorý dosadíme do klasického vzorca výpočtu obsahu kruhu:

S = π * r² = 3,14 * 4,95² = 3,14 * 24,50 ≈ 76,96

Výsledok: Obsah kruhu je približne 76,96 jednotiek².

Najčastejšie kladené otázky (FAQ)

Dajú sa použiť iné hodnoty π (napr. presnejšia 3,14159 alebo symbol π)?

Áno, niektoré skripty môžu ponúkať možnosť prepnutia medzi zaokrúhlenou hodnotou 3,14 a presnejšou desatinnou hodnotou alebo symbolom π. Presnosť výsledku tým mierne narastie. Naša kalkulačka pracuje so 14 miestnym symbolom π.

Prečo je výhodné poznať viacero metód výpočtu obsahu kruhu?

V praxi nemusíme mať vždy rovnaký typ vstupných údajov – raz poznáme priemer, inokedy polomer, obvod, alebo súradnice. Preto je užitočné vedieť rôzne prístupy, aby sme vedeli obsah kruhu dopočítať inými spôsobmi.

Je rozdiel medzi obsahom kruhu a obsahom kružnice?

Áno. Obsah sa počíta len pre kruh, čo je plošná oblasť. Kružnica je len obvod (čiara) a nemá obsah. Mnoho ľudí si tieto pojmy zamieňa.

Ako sa líši výpočet obsahu kruhu v rôznych jednotkách (mm, cm, m)?

Naša kalkulačka vypočíta správne výsledky v jednotkách, ktoré zvolíme aj spolu s prevodom.

Môžem použiť túto kalkulačku aj na technické výpočty v inžinierstve alebo stavebníctve?

Áno. Naša kalkulačka ale momentálne nezaokrúhľuje podľa nami stanovených kritérií. Môžeme si ale pomerne presný výsledok zaokrúhliť podľa uváženia mimo kalkulačky.

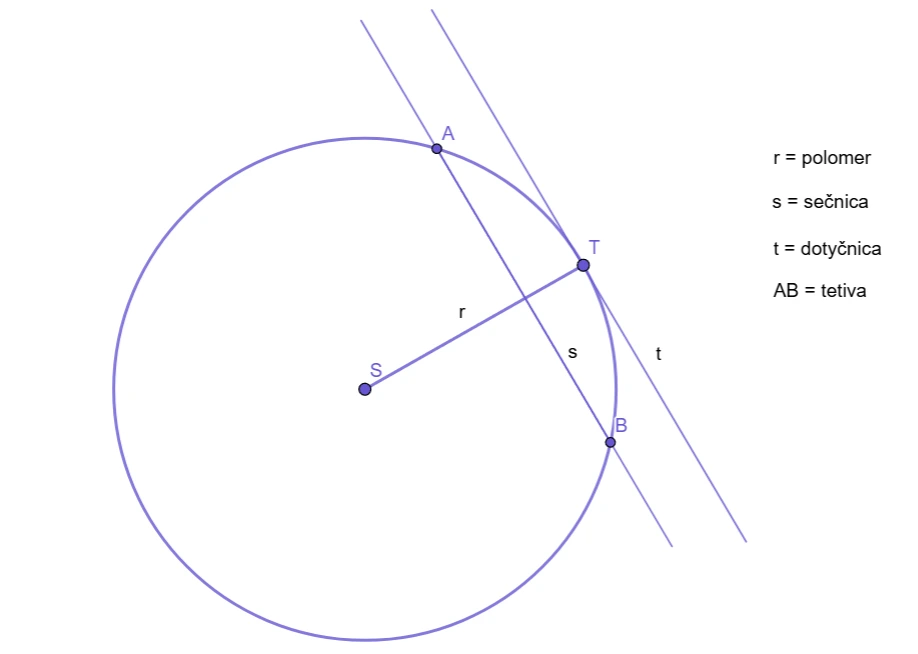
Vlastnosti kruhu

kruh je množina všetkých bodov v rovine, ktorých vzdialenosť od pevného bodu S je menšia, nanajvýš rovná polomeru „r“,
má nekonečne veľa osí súmernosti, pretože každá priamka prechádzajúca jeho stredom ho rozdeľuje na dve rovnaké polovice,
dotyčnica „t“ je kolmá na polomer „r“ v bode dotyku „T“,
sečnica „s“ je priamka, ktorá pretína kružnicu v dvoch bodoch A, B,
prienik sečnice a kruhu je tetiva kružnice „AB”.

Zdroje:

Kruh: https://cs.wikipedia.org/wiki/Kruh
ČERETKOVÁ, Soňa – ŠEDIVÝ, Ondrej – TEPLIČKA, Ivan. Matematika pre 8. Ročník základnej školy a 3. Ročník gymnázia s osemročným štúdiom, 2. časť. 96 s. Prvé vydanie, 2023. ISBN: 978-80-10-04149-7
ŽABKA, Ján – ČERNEK, Pavol. 2011. Matematika pre 8. ročník ZŠ a 3. ročník gymnázií s osemročným štúdiom. 1. vyd. Bratislava: Orbis Pictus Istropolitana, 2012. 143 s. ISBN 978-80-8120-125-7
Kruh a kružnica: https://www.dobre-napady.sk/pre-skolakov/tipy-pre-skolakov/kruh-a-kruznica