Obsah lichobežníka (kalkulačka)

Obsah lichobežníka predstavuje veľkosť plochy, ktorú lichobežník zaberá. Kalkulačka umožňuje výpočet obsahu na základe rôznych vstupov – od známych základní a výšky, cez súradnice vrcholov až po strednú priečku.

Ak poznáme dĺžky oboch základní a výšku

Ak poznáme dĺžky všetkých strán a výška nie je známa (rovnoramenný lichobežník)

Ak poznáme súradnice všetkých 4 vrcholov

Ak poznáme dĺžku strednej priečky a výšku

Ak potrebujete vypočítať obsah iných rovinných útvarov, skúste našu kalkulačku obsahu štvorca, alebo obdĺžnika.

Ako vypočítať obsah lichobežníka ak poznáme dĺžky oboch základní a výšku

zadáme dĺžku dolnej základne (a),
zadáme dĺžku hornej základne (c),
zadáme výšku (v) – teda kolmicu medzi základňami,
klikneme na tlačidlo „Vypočítať“,
kalkulačka zobrazí obsah lichobežníka v štvorcových jednotkách.

Vzorec pre výpočet obsahu lichobežníka ak poznáme dĺžky oboch základní a výšku

S = (a+c) * v / 2

Kde:

S predstavuje obsah lichobežníka,
a, c je dĺžka hornej a dolnej základne,
v je dĺžka výšky medzi základňami.

Príklad výpočtu obsahu lichobežníka ak poznáme dĺžky oboch základní a výšku

Vypočítajme plochu (obsah) lichobežníka, ak poznáme tieto údaje:

dĺžka spodnej základne lichobežníka (a) je 8 m,
dĺžka vrchnej základne lichobežníka (c) je 4 m,
výška medzi základňami je 3 m.

Všetky vstupy sú v metroch, preto nie je potrebné jednotky prevádzať. Ak sú vstupné hodnoty v rôznych jednotkách, musíme ich najprv zjednotiť na rovnaký typ (napríklad všetko v m).

Ak potrebujeme prepočítať jednotky, použijeme našu kalkulačku na prevod dĺžky. Výsledok môžeme tiež zaokrúhliť podľa potreby.

Riešenie:

Doplníme jednotlivé hodnoty do vzorca:

S = ((a+c) * v) / 2
S = ((8 + 4) * 3 ) / 2 = (12 * 3) / 2 = 36 / 2 = 18

Výsledok: Plocha lichobežníka je 18 m².

Kedy používame výpočet obsahu cez dĺžky základní a výšky

Výpočet obsahu lichobežníka pomocou dĺžok oboch základní a výšky patrí medzi najčastejšie používané spôsoby.

Tento prístup je ideálny vtedy, keď poznáme presné rozmery dolnej a hornej základne (označované ako a a c) a zároveň máme k dispozícii výšku (v), teda kolmú vzdialenosť medzi základňami.

Takýto výpočet využívame napríklad:

v geometrii a matematických úlohách na základných a stredných školách,
pri plánovaní a meraní výmery lichobežníkových pozemkov (napr. keď dve protiľahlé hranice sú rovnobežné),
v stavebníctve pri výpočte výmer atypických plôch – napríklad častí striech, svahov alebo pôdorysov miestností so šikmými stenami.

Ak máme k dispozícii tieto tri hodnoty, nie je potrebné poznať žiadne iné rozmery alebo uhly, čo z tejto metódy robí najpraktickejšiu možnosť pri výpočte obsahu bežného lichobežníka.

Najčastejšie kladené otázky (FAQ)

Platí táto metóda aj pri rovnoramennom lichobežníku?

Áno, pokiaľ poznáte základne a výšku, je jedno, či je lichobežník rovnoramenný alebo nie.

Ako zistím výšku lichobežníka, ak ju nepoznám?

Výšku je možné vypočítať napríklad pomocou trigonometrie alebo konštrukčne z náčrtu, no naša kalkulačka vyžaduje jej zadanú hodnotu.

Môže byť výška väčšia ako základne?

Áno, výška predstavuje kolmú vzdialenosť medzi základňami a môže byť väčšia než dĺžka základní.

Čo ak výsledok výpočtu vyjde ako desatinné číslo?

Desatinný výsledok je úplne v poriadku. Môžeme ho zaokrúhliť podľa potreby, napríklad na celé číslo alebo na dve desatinné miesta.

Prečo sa výsledok nemení, ak prehodím základne a a c?

Pretože vo vzorci sa základne sčítavajú a ich poradie nemá vplyv na výsledok. Matematicky: (a+c) = (c+a).

Je rozdiel medzi obsahom a výmerou lichobežníka?

V bežnej reči nie – oba pojmy označujú plochu. Z pohľadu matematiky je „obsah“ presnejší pojem, „výmera“ sa častejšie používa v súvislosti s výpočtom plochy pozemkov alebo plochami v technickej praxi.

Ako vypočítať obsah rovnoramenného lichobežníka zo známych strán (bez výšky)

zadáme dĺžku dolnej základne (a),
zadáme dĺžku hornej základne (c),
zadáme jednotnú dĺžku strán (b) a (d),
klikneme na tlačidlo „Vypočítať“,
kalkulačka zobrazí obsah lichobežníka v štvorcových jednotkách.

Vzorec výpočtu obsahu rovnoramenného lichobežníka zo známych strán (bez výšky)

Najprv musíme vypočítať neznámu výšku (v) medzi základňami:

v = √[ b² − ((a − c) / 2)² ]

Kde:

v je výška medzi základňami,
c je dĺžka hornej základne,
a je dĺžka dolnej základne,
b je dĺžka ramena (obidvoch ramien, teda aj “d”, ktoré vo vzorci nie je potreba uviesť, pretože je rovnaká ako “b”).

Po vypočítaní dĺžky výšky dosadíme do klasického vzorca pre výpočet obsahu lichobežníka:

S = (a + c) * v / 2

Kde:

S predstavuje obsah lichobežníka,
a, c je dĺžka hornej a dolnej základne,
v je dĺžka výšky medzi základňami.

Príklad výpočtu obsahu rovnoramenného lichobežníka zo známych strán (bez výšky)

Povedzme, že máme pozemok v tvare rovnoramenného lichobežníka a potrebujeme určiť jeho výmeru, ak vieme nasledovné údaje:

dĺžka dolnej základne (a) je 20 m,
dĺžka hornej základne (c) je 8 m,
ramená lichobežníka b a d sú zhodne po 7 metrov.

Vypočítajme plochu lichobežníka.

Najprv potrebujeme určiť výšku pomocou vzorca:

v = √[ b² − ((a − c) / 2)² ]

v = √[ 7² − ((20 − 8) / 2)² ]

v = √[ 49 − ((12) / 2)² ]

v = √[ 49 − (6)² ]

v = √[ 49 − 36 ]

v = √[ 13 ]

v ≈ 3,60

Výsledok: Výška medzi základňami lichobežníka je približne 3,60 m.

Vypočítanú výšku medzi základňami dosadíme do klasického vzorca:

S = ((a + c) * v) / 2

S = ((20 + 8) * 3,60) / 2

S = (28 * 3,60) / 2

S = 100,8 / 2

S = 50,4 m²

Výsledok: Plocha lichobežníka je približne 50,4 m².

Kedy používame výpočet obsahu rovnoramenného lichobežníka zo známych strán (bez výšky)

Tento spôsob výpočtu obsahu lichobežníka používame v situáciách, keď nepoznáme výšku (kolmú vzdialenosť medzi základňami), ale máme k dispozícii dĺžky všetkých štyroch strán – teda dolnej a hornej základne a oboch ramien.

Najčastejšie ide o rovnoramenný lichobežník, kde výšku vypočítame pomocou známych strán a následne použijeme vo vzorci pre obsah.

Výhodou tohto prístupu je, že nám stačí pásmo alebo plán so známymi dĺžkami strán a nemusíme priamo merať výšku, čo býva v teréne často problematické.

Takýto výpočet je vhodný napríklad:

keď poznáme rozmery parcely v tvare lichobežníka, ale nemáme informáciu o výške (napr. z geometrického plánu),
v technických výkresoch, kde sú uvedené len strany a nie výšky,
pri digitalizácii starých máp alebo výkresov, kde sa pracuje len s dĺžkami strán,
v geometrii, keď je potrebné počítať výmeru na základe údajov zadaných ako štyri strany.

Najčastejšie kladené otázky (FAQ)

Musia byť ramená naozaj úplne rovnaké, aby tento výpočet fungoval?

Nie nutne, ale výpočet výšky cez uvedený vzorec je presný iba vtedy, keď sú ramená lichobežníka rovnaké (rovnoramenný lichobežník). Ak sa ramená líšia, výpočet výšky touto metódou nebude správny.

Čo sa stane, ak zadám dĺžky strán, ktoré nevedú k platnému lichobežníku?

Kalkulačka by mala vyhodiť chybu alebo výpočet nebude možný (napr. ak pod odmocninou vznikne záporné číslo). Takéto zadané hodnoty narušujú geometriu lichobežníka.

Môžem použiť tento výpočet aj na výšku, ak mi vyjde ako zlomok alebo desatinné číslo?

Áno. Výška môže byť v desatinných číslach, čo je úplne bežné. Môžeš ju nechať ako je, alebo ju zaokrúhliť podľa požadovanej presnosti.

Existuje aj spôsob výpočtu obsahu bez výšky a bez rovnosti ramien?

Áno, ale je to zložitejšie. Pri nerovnoramennom lichobežníku možno použiť Bretschneiderov alebo Brahmaguptov vzorec, ktorý vyžaduje aj uhly alebo uhlopriečky.

Môžem použiť iné jednotky ako metre?

Áno, ale všetky vstupy musia byť v rovnakej jednotke. Kalkulačka neprevádza automaticky cm na m alebo mm na cm – jednotky si musíš zjednotiť sám pred výpočtom.

Ako vypočítať obsah lichobežníka ak poznáme súradnice všetkých 4 vrcholov

zadáme súradnice bodu A (x₁,y₁),
zadáme súradnice bodu B (x₂,y₂),
zadáme súradnice bodu C (x₃,y₃),
zadáme súradnice bodu D (x₄,y₄),
klikneme na tlačidlo „Vypočítať“,
kalkulačka zobrazí obsah lichobežníka v štvorcových jednotkách.

Vzorec pre výpočet obsahu lichobežníka ak poznáme súradnice všetkých 4 vrcholov

Shoelace vzorec: S = ½ * |(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) − (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)|

Kde:

x₁,x₂,x₃,x₄ sú x-ové súradnice jednotlivých vrcholov lichobežníka,
y₁,y₂,y₃,y₄ sú y-ové súradnice tých istých vrcholov (v rovnakom prostredí).

Dbáme na to, aby sme zadali body v poradí podľa obvodu lichobežníka (napr. v smere hodinových ručičiek), inak môže výpočet vyjsť záporný alebo nesprávny.

Príklad výpočtu obsahu lichobežníka ak poznáme súradnice všetkých 4 vrcholov

Majme lichobežník definovaný vrcholmi v rovine so súradnicami (v metroch):

A = (2,1)
B = (6,1)
C = (5,4)
D = (3,4)

Vypočítajme jeho obsah dosadením do Shoelace vzorca:

S = ½ * |(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) − (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)|

S = ½ * |(2*1 + 6*4 + 5*4 + 3*1) – (6*1 + 5*1 + 3*4 + 2*4)|

S = ½ * |(2 + 24 + 20 + 3) – (6 + 5 + 12 + 8)

S = ½ * |49 – 31|

S = ½ * 18 = 9

Výsledok: Obsah lichobežníka je 9 m².

Kedy používame výpočet obsahu lichobežníka ak poznáme súradnice všetkých 4 vrcholov

Tento spôsob výpočtu sa používa najmä vtedy, keď poznáme presné súradnice všetkých štyroch vrcholov lichobežníka v rovine (napríklad z mapy, GPS merania alebo technického výkresu), ale nepoznáme výšky ani dĺžky strán.

Výhodou tejto metódy je, že nepotrebujeme žiadne konštrukcie, prevody ani merania – stačí nám tabuľka alebo výpis bodov v tvare (x,y).

Shoelace vzorec (alebo aj „determinantový vzorec“) umožňuje vypočítať obsah priamo zo súradníc, bez nutnosti poznať, ktoré strany sú základne alebo ramená.

Tento výpočet je užitočný napríklad:

pri výpočte výmery pozemku podľa katastrálnych súradníc,
v geografických informačných systémoch (GIS) a mapových podkladoch,
v CAD programoch a technických nákresoch, kde sú body zadané ako súradnice,
pri meraniach dronmi alebo totálnou stanicou, ktoré poskytujú výstup v podobe bodov v rovine,
v školských úlohách, kde sa pracuje s analytickou geometriou.

Shoelace algoritmus funguje spoľahlivo pre akýkoľvek konvexný alebo konkávny štvoruholník, pokiaľ máme vrcholy zadané v správnom poradí (v smere alebo proti smeru hodinových ručičiek). Táto metóda je flexibilná a univerzálna bez ohľadu na orientáciu alebo tvar lichobežníka.

Najčastejšie kladené otázky (FAQ)

Je možné Shoelace vzorec použiť aj pre iné štvoruholníky než lichobežník?

Áno, Shoelace vzorec funguje pre akýkoľvek štvoruholník, pokiaľ sú známe súradnice všetkých vrcholov a tie sú zadané v správnom poradí. Je vhodný aj pre nepravidelné mnohouholníky.

Dá sa výsledok výpočtu pomocou súradníc overiť iným spôsobom?

Áno, ak poznáme aspoň dve základne a výšku, môžeme si vypočítať obsah cez klasický vzorec a porovnať ho s výsledkom Shoelace metódy. Ideálne pri validácii dát.

Čo sa stane, ak zadám body v zlom poradí?

Výsledok môže vyjsť ako záporné číslo alebo nesprávna plocha. Vzorec predpokladá uzavretý polygon v určitom poradí. Vždy preto zadávaj body podľa obvodu lichobežníka.

Musia byť body v súradniciach zadané ako celé čísla?

Nie, môžeme zadať aj desatinné hodnoty (napr. 3,5 alebo 6.25). Výpočet funguje rovnako presne, pokiaľ sú hodnoty korektne zadané.

Je rozdiel medzi výpočtom cez Shoelace a cez determinant?

Nie, Shoelace je vlastne upravený determinatový výpočet pre plochu mnohouholníka. Výsledok bude ten istý, len forma výpočtu sa líši.

Ako vypočítať obsah lichobežníka cez strednú priečku a výšku

zadáme dĺžku strednej priečky (m),
zadáme výšku medzi základňami (v),
klikneme na tlačidlo „Vypočítať“,
kalkulačka zobrazí obsah lichobežníka v štvorcových jednotkách.

Vzorec pre výpočet obsahu lichobežníka cez strednú priečku a výšku

S = m x v

Kde:

m je dĺžka strednej priečky, ktorú vypočítame ako aritmetický priemer základní: m = (a + c) / 2,
v je výška medzi základňami.

Príklad výpočtu obsahu lichobežníka cez strednú priečku a výšku

Máme lichobežník, pri ktorom poznáme tieto údaje:

dĺžka strednej priečky (m) je 9 metrov,
výška medzi základňami (v) sú 4 metre.

Vypočítajme obsah lichobežníka.

Riešenie:

Dosadíme do vzorca:

S = m x v

S = 9 x 4 = 36

Výsledok: Obsah lichobežníka je 36 m².

Kedy používame výpočet obsahu lichobežníka ak poznáme dĺžku strednej priečky a výšku

Tento spôsob výpočtu používame v situáciách, keď nemáme priamo známe dĺžky oboch základní lichobežníka, ale vieme, aká je stredná priečka (úsečka spájajúca stredy ramien) a poznáme výšku medzi základňami.

Je to ideálny spôsob výpočtu najmä vtedy, keď:

rozmery základní nie sú priamo dostupné (napr. pri náčrtoch alebo plánikoch),
stredná priečka bola zmeraná ako priemer oboch základní (napr. z geometrického alebo stavebného výkresu),
výpočet chceme urýchliť bez potreby zisťovania dĺžok strán zvlášť.

Metóda je užitočná napríklad:

pri rýchlych odhadoch plochy, kde je známa len priemerná dĺžka základní,
v geodézii alebo mapovaní, kde výpočtový softvér poskytuje strednú priečku ako súčasť výstupu,
pri grafickom návrhu alebo stavebnom pláne, kde sa pracuje so stredmi strán namiesto celých rozmerov.

Výhodou tejto metódy je jej jednoduchosť – obsah vypočítame len ako súčin strednej priečky a výšky, bez potreby sčítavania alebo delenia. To z nej robí praktický nástroj pri orientačných aj technických výpočtoch.

Najčastejšie kladené otázky (FAQ)

Je stredná priečka vždy rovnobežná so základňami?

Áno, strednú priečku lichobežníka definujeme ako úsečku spájajúcu stredy ramien a je vždy rovnobežná s oboma základňami.

Ako zistím strednú priečku, ak poznám len základne?

Strednú priečku vypočítame ako priemer dĺžok základní: m = (a + c) / 2. Táto hodnota sa dá použiť priamo vo výpočte obsahu.

Čo ak sú základne rovnaké – môžem ešte hovoriť o strednej priečke?

Áno, stredná priečka v takom prípade bude mať rovnakú dĺžku ako základne. V tomto prípade ide o rovnobežník, ale výpočet ostáva rovnaký.

Je táto metóda vhodná aj pre konkávne lichobežníky?

Nie, tento výpočet sa vzťahuje len na konvexné lichobežníky, kde je stredná priečka jednoznačne definovaná.

Dá sa z výpočtu spätne určiť dĺžka jednej základne?

Áno, ak poznáme strednú priečku a jednu základňu, vieme druhú základňu dopočítať z rovnice m = (a + c) / 2.

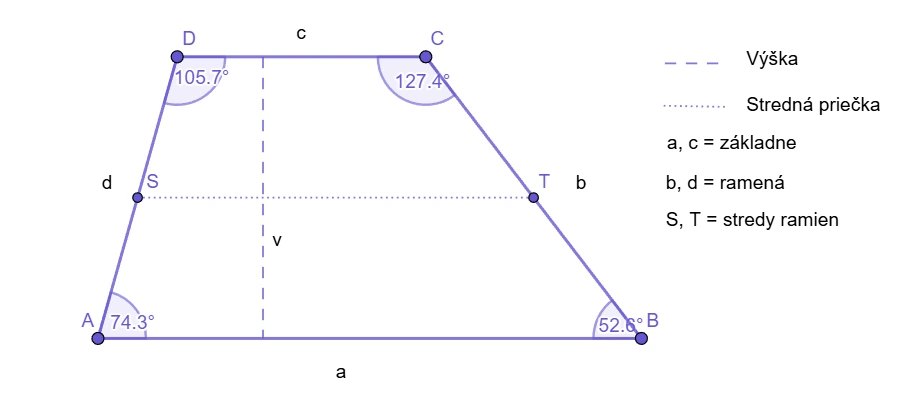
Vlastnosti lichobežníka

základne sú rovnobežné,
zvyšné strany (ramená) sú rôznobežné,
spojnica stredov ramien je stredná priečka, ktorá je rovnobežná so základňami a jej dĺžka je aritmetickým priemerom dĺžok základní,
súčet vnútorných uhlov je vždy 360°,
rovnoramenný lichobežník je osovo súmerný a môže byť tetivovým štvoruholníkom (môže byť vpísaný do kruhu).

Zdroje:

Lichobežník: https://sk.wikipedia.org/wiki/Lichobe%C5%BEn%C3%ADk
Lichobenžík: Základné informácie a vlastnosti: https://www.priklady.com/sk/index.php/lichobeznik
ČERETKOVÁ, Soňa – ŠEDIVÝ, Ondrej – TEPLIČKA, Ivan. Matematika pre 8. Ročník základnej školy a 3. Ročník gymnázia s osemročným štúdiom, 2. časť. 96 s. Prvé vydanie, 2023. ISBN: 978-80-10-04149-7
Shoelace formula: https://en.wikipedia.org/wiki/Shoelace_formula