Obsah štvorca (kalkulačka)

Kalkulačka obsahu štvorca nám umožňuje vypočítať obsah štvorca pomocou rôznych vzorcov, napríklad zo strany, uhlopriečky, pomocou súradnicových bodov a pod.

Obsah štvorca so známou stranou

Obsah štvorca so známou uhlopriečkou

Obsah štvorca pomocou tzv. Shoelace vzorca (determinantový vzorec)

Obsah štvorca pomocou výpočtu dĺžky strany zo súradníc

Obsah štvorca ak máme súradnice krajných bodov uhlopriečky (napr. A a C)

Obsah štvorca ak máme polomer vpísanej kružnice

Obsah štvorca ak máme polomer opísanej kružnice

Vzorce pre výpočet obsahu štvorca

Ak je známa dĺžka strany štvorca

S = a²

Kde:

• a = dĺžka strany štvorca.

Príklad: Ak máme dĺžku strany štvorca 3 cm, tak obsah (S) = 3² = 9 cm².

Ak je známa uhlopriečka štvorca

S = d²/2

Kde:

• d = dĺžka uhlopriečky.

Príklad:

Máme zadanú dĺžku uhlopriečku 4 cm.

Dosadníme do vzorca S = 4² / 2 =  8 cm².

Výpočet pomocou tzv. Shoelace vzorca (determinantový vzorec)

S = ½ × |(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) − (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)|

Kde:

• (x_i,y_i) sú súradnice vrcholov v poradí (v smere alebo proti smeru hodinových ručičiek).

Príklad: 

Máme body:

A (2, 1)

B (5, 1)

C (5, 4)

D (2, 4)

Dosadíme do vzorca:

S = ½ x ∣(2×1+5×4+5×4+2×1)−(1×5+1×5+4×2+4×2)∣

S = ½ x ∣(2+20+20+2)−(5+5+8+8)∣

S = ½ x ∣44−26∣

S = ½ x 18

S = 9

Výsledok: Obsah štvorca podľa Shoelace vzorca je 9 štvorcových jednotiek.

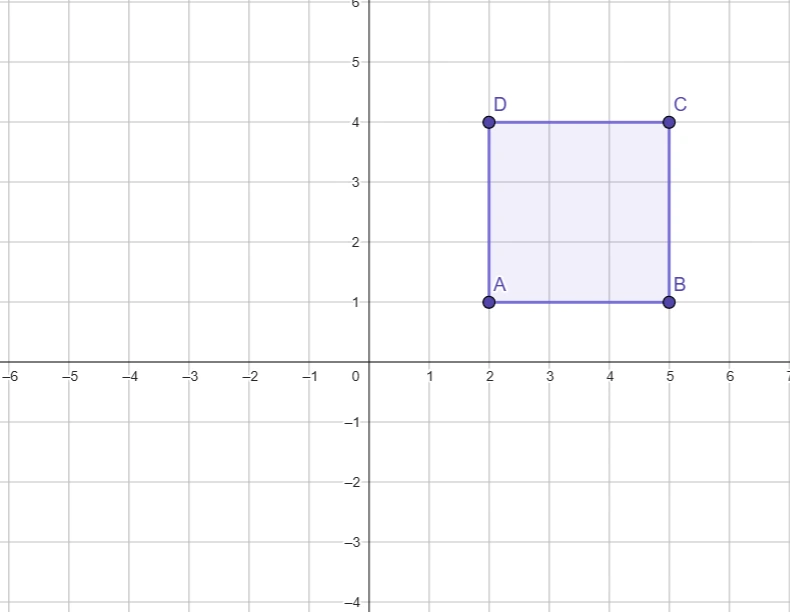
Výpočet dĺžky strany zo súradníc

Dĺžka strany (a) = √[ (x₂ − x₁)² + (y₂ − y₁)² ]

Kde:

• Ak máme dve susedné body (napr. A = (x₁, y₁), B = (x₂,y₂)
• Ak vypočítame stranu zo súradníc, následne použijeme klasický vzorec S = a² 

Príklad:

Vypočítajte dĺžku strany štvorca, ak sú dané súradnice dvoch susedných vrcholov:

A (2, 1)

B (5, 1)

Dĺžka strany (a) = √[ (x₂ − x₁)² + (y₂ − y₁)² ]

Dĺžka strany (a) = √[ (5 − 2)² + (1 − 1)² ]

Dĺžka strany (a) = √[ 9 + 0 ]

Dĺžka strany (a) = √9

Dĺžka strany (a) = 3 jednotky

Následne vypočítame obsah štvorca pomocou vzorca S = a² = 3² = 9 štvorcových jednotiek.

Ak máme súradnice krajných bodov uhlopriečky (napr. A a C)

Uhlopriečka vo štvorci prechádza stredom a obe uhlopriečky sú rovnaké, sú na seba kolmé a navzájom sa rozpoľujú. Uhlopriečku vypočítame pomocou Pytagorovej vety (c² = a² + b²). Následne vieme použiť klasický vzorec S = d² / 2

Príklad: 

Súradnice bodu A a C v cm.

A = (2, 1)

C= (5, 1)

Výpočet dĺžky uhlopriečky pomocou Pytagorovej vety:

d = √[ (x₂ − x₁)² + (y₂ − y₁)² ]

d =  √[ (5 − 2)² + (1 − 1)² ]

d =  √[ 3² + 0² ]

d = √9

d = 3 cm

Pre výpočet obsahu štvorca následne použijeme S = d² / 2 = 3² / 2 = 9 / 2 = 4,5 cm².

Ak máme polomer vpísanej kružnice

Ak poznáme polomer vpísanej kružnice, najprv vypočítame dĺžku strany štvorca podľa vzorca:

Strana štvorca (a) = 2 x r

Následne, keď už poznáme stranu štvorca (a), dosadíme ju do základného vzorca pre výpočet obsahu štvorca:

Obsah štvorca = a²

Kde:

• a = strana štvorca,
• r = polomer vpísanej kružnice.

Príklad:

Potrebujeme vypočítať obsah štvorca, ak poznáme priemer vpísanej kružnice, ktorý je 10 cm.

Riešenie:

Najprv vypočítame polomer:

r = priemer / 2 = 10 cm / 2 = 5 cm

Potom dosadíme do vzorca pre výpočet strany štvorca:

a = 2 × r = 2 × 5 cm = 10 cm

Obsah štvorca vypočítame ako druhú mocninu dĺžky jeho strany:

S = a² = 10² = 100 cm².

Ak máme polomer opísanej kružnice

Rovnako ako v prípade vpísanej kružnice, aj tu najprv potrebujeme vypočítať dĺžku strany štvorca, tentokrát však podľa iného vzorca:

Strana štvorca (a) = r x √2

Po výpočte strany štvorca ju dosadíme do základného vzorca pre výpočet obsahu štvorca:

Obsah štvorca = a²

Kde:

• a = strana štvorca,
• r = polomer opísanej kružnice.

Príklad:

Poznáme polomer opísanej kružnice: r = 7 cm. Potrebujeme vypočítať obsah štvorca.

Najprv vypočítame dĺžku strany štvorca:

a = 7 x √2 ≈ 9,9 cm.

Potom vypočítame obsah:

S = a² = 9,9² ≈ 98 cm².

Praktický príklad obsahu štvorca

Renovujeme podlahu a chceme použiť malé dlaždice so šírkou 4×4 dm, a vieme, že medzi dlaždicami budeme mať špáry so šírkou 3 mm. Naša miestnosť má rozmery 5x5m. 

Koľko potrebujeme kusov dlaždíc, ak vezmeme do úvahy aj špáry medzi nimi pre pokrytie celej miestnosti? Príklad počíta s tým, že špára sa počíta len raz medzi dvoma dlaždicami (tzn. nie okolo celej).

Riešenie:

• Výpočet jedného “modulu” (dlaždica + špára)
  • 4 dm + 0,3 cm = 4,3 dm = 43 cm
• Počet “modulov” na jednu stranu miestnosti
  • 5 m = 500 cm
  • 500 / 43 ≈ 11,627 = 12 (zaokrúhľujeme nahor, pretože potrebujeme prekryť celú plochu miestnosti)
  • 12 dlaždíc potrebujeme na jednu stranu
• Celkový počet dlaždíc
  • 12 x 12 = 144 kusov

Odpoveď: Na pokrytie štvorcovej miestnosti s rozmermi 5 x 5 metrov, kde každá dlaždica má rozmer 4 x 4 dm a špárou 3 mm medzi každou dlaždicou a aj pri stene, budeme potrebovať približne 144 kusov dlaždíc.

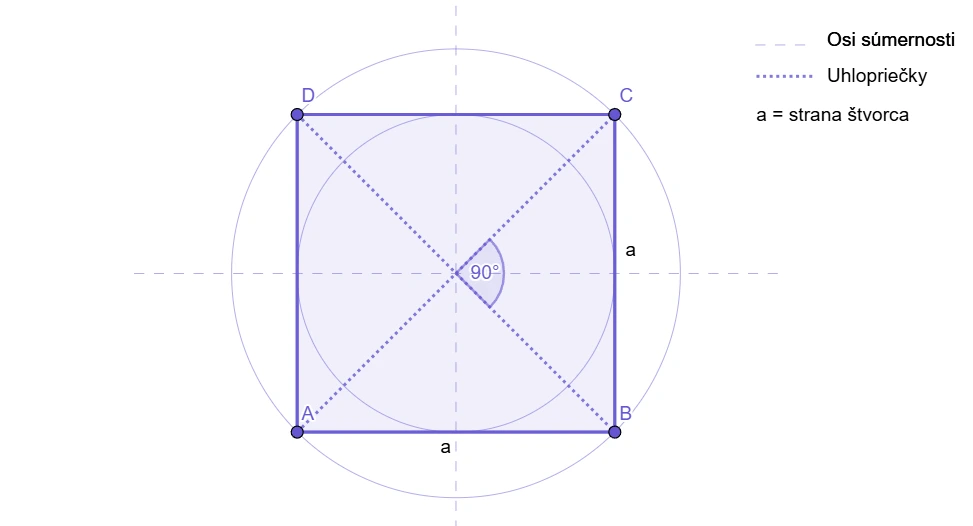
Vlastnosti štvorca

• všetky strany sú rovnako dlhé,
• susedné strany sú na seba kolmé,
• protiľahlé strany sú rovnobežné,
• uhlopriečky majú rovnakú dĺžku a rozpoľujú sa v strede,
• uhlopriečky zvierajú pravý uhol,
• priesečník uhlopriečok je stredom vpísanej a opísanej kružnice,
• má štyri osi súmernosti.

Obsah štvorca je plocha, ktorú zaberá jeho vnútorná časť vrátane obvodových čiar.

Najčastejšie otázky pre výpočet obsahu štvorca

Zdroje:

• Štvorec – vzorce a vzťahy: https://pohodovamatematika.sk/stvorec-vzorce-a-vztahy.html
• Štvorec: https://sk.wikipedia.org/wiki/%C5%A0tvorec
• Cartesian coordinate system: https://en.wikipedia.org/wiki/Cartesian_coordinate_system
• Shoelace formula: https://en.wikipedia.org/wiki/Shoelace_formula